
【题目】记无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() ,则称
,则称![]() 是
是![]() “极差数列”.
“极差数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“极差数列”仍是
的“极差数列”仍是![]() ;
;
(3)求证:若数列![]() 是等差数列,则数列
是等差数列,则数列![]() 也是等差数列.
也是等差数列.
【答案】(1)![]() (2)证明见解析(3)证明见解析
(2)证明见解析(3)证明见解析
【解析】
(1)由![]() 是递增数列,得
是递增数列,得![]() ,由此能求出
,由此能求出![]() 的前
的前![]() 项和.
项和.
(2)推导出![]() ,
,![]() ,由此能证明
,由此能证明![]() 的“极差数列”仍是
的“极差数列”仍是![]() .
.
(3)证当数列![]() 是等差数列时,设其公差为
是等差数列时,设其公差为![]() ,
,![]()
![]() ,
,![]() 是一个单调递增数列,从而
是一个单调递增数列,从而![]() ,
,![]() ,由
,由![]() ,
,![]() ,
,![]() ,分类讨论,能证明若数列
,分类讨论,能证明若数列![]() 是等差数列,则数列
是等差数列,则数列![]() 也是等差数列.
也是等差数列.
(1)解:∵无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,
,![]() ,
,![]() ,
,
![]() 是递增数列,∴
是递增数列,∴![]() ,
,
∴![]() 的前
的前![]() 项和
项和![]() .
.
(2)证明:∵![]() ,
,
![]() ,
,
∴![]()
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 的“极差数列”仍是
的“极差数列”仍是![]()
(3)证明:当数列![]() 是等差数列时,设其公差为
是等差数列时,设其公差为![]() ,
,
![]()
![]() ,
,
根据![]() ,
,![]() 的定义,得:
的定义,得:
![]() ,
,![]() ,且两个不等式中至少有一个取等号,
,且两个不等式中至少有一个取等号,
当![]() 时,必有
时,必有![]() ,∴
,∴![]() ,
,
∴![]() 是一个单调递增数列,∴
是一个单调递增数列,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() 是等差数列,
是等差数列,
当![]() 时,则必有
时,则必有![]() ,∴
,∴![]() ,
,
∴![]() 是一个单调递减数列,∴
是一个单调递减数列,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .∴
.∴![]() 是等差数列,
是等差数列,
当![]() 时,
时,![]()
![]() ,
,
∵![]() ,
,![]() 中必有一个为0,
中必有一个为0,
根据上式,一个为0,为一个必为0,
∴![]() ,
,![]() ,
,
∴数列![]() 是常数数列,则数列
是常数数列,则数列![]() 是等差数列.
是等差数列.
综上,若数列![]() 是等差数列,则数列
是等差数列,则数列![]() 也是等差数列.
也是等差数列.


科目:高中数学 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,点E在AB上,AE=2EB=2,且DE⊥AB.以DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.
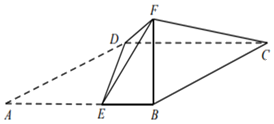
(1)求证:平面BFC⊥平面BCDE;
(2)若直线DF与平面BCDE所成角的正切值为![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的正视图是一个底边长为4腰长为3的等腰三角形,图1、图2分别是四棱锥
的正视图是一个底边长为4腰长为3的等腰三角形,图1、图2分别是四棱锥![]() 的侧视图和俯视图.
的侧视图和俯视图.
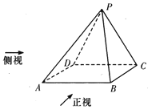
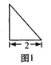
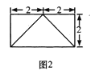
(1)求证:![]() ;
;
(2)求四棱锥![]() 的体积及侧面积.
的体积及侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某大学学生的某天上网的时间,随机对![]() 名男生和
名男生和![]() 名女生进行了不记名的问卷调查.得到了如下的统计结果:
名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
上网时间(分钟) |
|
|
|
|
|
人数 |
|
|
|
|
|
表2:女生上网时间与频数分布表
上网时间(分钟) |
|
|
|
|
|
人数 |
|
|
|
|
|
(1)用分层抽样在![]() 选取
选取![]() 人,再随机抽取
人,再随机抽取![]() 人,求抽取的
人,求抽取的![]() 人都是女生的概率;
人都是女生的概率;
(2)完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“大学生上网时间与性别有关”?
的把握认为“大学生上网时间与性别有关”?
上网时间少于 | 上网时间不少于 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: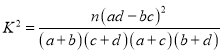
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为![]() ,(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C1:ρ=2cosθ,
,(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C1:ρ=2cosθ,![]() .
.
(1)求C1与C2交点的直角坐标;
(2)若直线l与曲线C1,C2分别相交于异于原点的点M,N,求|MN|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今有6个人组成的旅游团,包括4个大人,2个小孩,去庐山旅游,准备同时乘缆车观光,现有三辆不同的缆车可供选择,每辆缆车最多可乘3人,为了安全起见,小孩乘缆车必须要大人陪同,则不同的乘车方式有_____种.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com