
 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(| 6 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| MN |
| sin∠MON |
| ON |
| sin∠OMN |
| ||||
| sin105° |
2
| ||
| sin∠OMN |
| ||
| 2 |
| OM |
| sin∠ONM |
| ON |
| sin∠OMN |
| 2 | ||
|
2
| ||
| 3 |
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
| 2 |
2
| ||
| x |
2
| ||
| 3x |
| tanα-tanβ |
| 1+tanα•tanβ |
4
| ||
| 3 |
| 1 | ||
x+
|
| 4 |
| x |
x•
|
| ||
| 3 |


科目:高中数学 来源: 题型:解答题
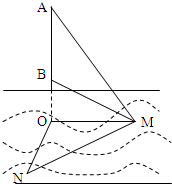 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(
 )海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=
)海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON= 海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.
海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.查看答案和解析>>
科目:高中数学 来源:2013年江苏省高考数学模拟试卷(五)(解析版) 题型:解答题
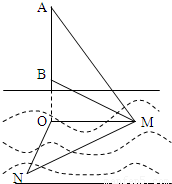 如图,某海域中有甲、乙两艘测量船分别停留在相距(
如图,某海域中有甲、乙两艘测量船分别停留在相距(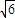
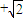 )海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=2
)海里的M,N两地,他们在同时观测岛屿上中国移动信号塔AB,设塔底延长线与海平面交于点O.已知点M在点O的正东方向,点N在点O的南偏西15°方向,ON=2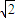 海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.
海里,在M处测得塔底B和塔顶A的仰角分别为30°和60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com