
(10分)选修4-1:几何证明选讲.
已知C点在圆O直径BE的延长线上,CA切圆O于A点,DC是 的平分线交AE于点F,交AB于D点.
的平分线交AE于点F,交AB于D点.

(1) 求 的度数;
的度数;
(2) 若AB=AC,求AC:BC.
(1) ;(2)
;(2) 
【解析】本题考查的知识点是圆周角定理,三角形外角定理,弦切角定理,相似三角形的证明及性质等,本题中未给出任何角的度数,故建立∠ADF必为特殊角,从而根据图形分析角∠ADF的大小,进而寻出解答思路是解题的关键.
(I)根据AC为圆O的切线,结合弦切角定理,我们易得∠B=∠EAC,结合DC是∠ACB的平分线,根据三角形外角等于不相邻两个内角的和,我们易得∠ADF=∠AFD,进而结合直径所对的圆周角为直角,求出∠ADF的度数;
(II)若AB=AC,结合(1)的结论,我们易得∠ACB=30°,根据顶角为120°的等腰三角形三边之比为:1:1: 3,易得答案.
解: AC为圆O的切线,∴
AC为圆O的切线,∴ 又知,DC是
又知,DC是 的平分线,
的平分线,
∴ ∴
∴
即  又因为BE为圆O的直径, ∴
又因为BE为圆O的直径, ∴
∴
(2)
 ,
, ,∴
,∴ ∽
∽ ∴
∴
又 AB=AC, ∴
AB=AC, ∴ ,
,
∴在Rt⊿ABE中, 


科目:高中数学 来源:2011-2012学年河北省高三第一次高考仿真测试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-1:几何证明选讲
已知 为半圆
为半圆 的直径,
的直径, ,
, 为半圆上一点,过点
为半圆上一点,过点 作半圆的切线
作半圆的切线 ,过点
,过点 作
作 于
于 ,交半圆于点
,交半圆于点 ,
, .
.

(Ⅰ)求证: 平分
平分 ;
;
(Ⅱ)求 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省镇平一高高三下学期第四次周考文科数学试卷 题型:解答题
(本小题满分10分)选修4-1:几何证明选讲
如图,锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.
(Ⅰ)求证:四点A,I,H,E共圆;
(Ⅱ)若∠C=50°,求∠IEH的度数.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年山西省忻州市高三第一次联考数学理卷 题型:解答题
【题文】(本题满分10分) 选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,AH=2.
(1)求DE的长;
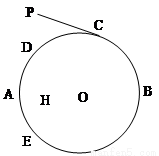 (2)延长ED到P,过P作圆O的切线,切点为C,若PC=2
(2)延长ED到P,过P作圆O的切线,切点为C,若PC=2 ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山西省忻州市高三第一次联考数学文卷 题型:解答题
(本题满分10分) 选修4-1:几何证明选讲
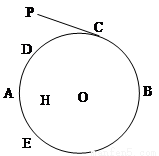
如图,圆O的直径AB=10,弦DE⊥AB于点H,
AH=2.
(Ⅰ)求DE的长;
(Ⅱ)延长ED到P,过P作圆O的切线,切点为C,
若PC=2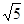 ,求PD的长.
,求PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com