
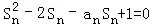 ,n=1,2,3
,n=1,2,3 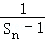 }是等差数列;
}是等差数列;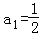 ,
,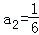 ;(2)SnSn﹣1﹣2Sn+1=0;(3)
;(2)SnSn﹣1﹣2Sn+1=0;(3)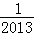 .
.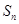 与
与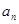 的关系式求
的关系式求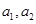 的值;(2)当
的值;(2)当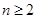 时,把
时,把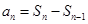 代入已知关系式可得与
代入已知关系式可得与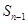 的关系式,再由此关系式,去凑出
的关系式,再由此关系式,去凑出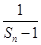 和
和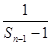 ,可得所求数列
,可得所求数列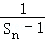 是等差数列,进而得通项
是等差数列,进而得通项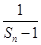 的表达式,从而得
的表达式,从而得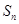 的表达式;(3)由(2)中
的表达式;(3)由(2)中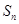 的表达式易求S1•S2•S3 S2011•S2012的值.
的表达式易求S1•S2•S3 S2011•S2012的值.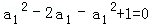 ,解得
,解得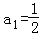 ,
,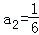 . (4分)
. (4分)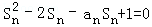 ,
,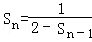 , (7分)
, (7分)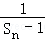 =﹣1+
=﹣1+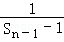 ,
,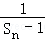 }是首项为
}是首项为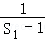 =﹣2,公差为﹣1的等差数列, (10分)
=﹣2,公差为﹣1的等差数列, (10分)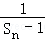 =﹣2+(n﹣1)•(﹣1)=﹣n﹣1,∴Sn=
=﹣2+(n﹣1)•(﹣1)=﹣n﹣1,∴Sn=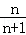 . (12分)
. (12分) •
•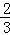 •
•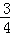 •
•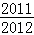 •
•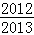 =
=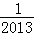 . (14分)
. (14分)

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源:不详 题型:解答题
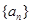 的前
的前 项和为
项和为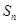 ,
,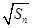 是
是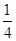 与
与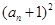 的等比中项.
的等比中项.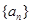 是等差数列;
是等差数列;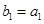 ,且
,且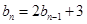 ,求数列
,求数列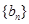 的通项公式;
的通项公式;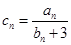 ,求数列
,求数列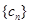 的前
的前 项和
项和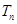 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com