
分析 (1)求出函数f(x)的定义域,再利用奇偶性的定义判断f(x)是定义域上的偶函数;
(2)f(x)在[0,+∞)上是单调减函数,用定义证明即可;
(3)根据题意,把不等式f(1-t)<f(t)化为|1-t|>|t|,求出解集即可.
解答 解:(1)∵函数f(x)=$\frac{{2}^{x}}{{4}^{x}+1}$,x∈R,
∴对任意x∈R,f(-x)=$\frac{{2}^{-x}}{{4}^{-x}+1}$=$\frac{{2}^{-x}{•4}^{x}}{{(4}^{-x}+1){•4}^{x}}$=$\frac{{2}^{x}}{{4}^{x}+1}$=f(x),
∴f(x)是R上的偶函数;
(2)f(x)在[0,+∞)上是单调减函数,用定义证明如下;
任取x1、x2∈[0,+∞),且x1<x2,
则f(x1)-f(x2)=$\frac{{2}^{{x}_{1}}}{{4}^{{x}_{1}}+1}$-$\frac{{2}^{{x}_{2}}}{{4}^{{x}_{2}}+1}$=$\frac{{(2}^{{x}_{2}}{-2}^{{x}_{1}}){(2}^{{x}_{1}{+x}_{2}}+1)}{{(4}^{{x}_{1}}+1){(4}^{{x}_{2}}+1)}$;
∵0≤x1<x2,∴${2}^{{x}_{2}}$-${2}^{{x}_{1}}$>0,${2}^{{x}_{1}{+x}_{2}}$+1>0,${4}^{{x}_{1}}$+1>0,${4}^{{x}_{2}}$+1>0;
∴f(x1)-f(x2)>0,
即f(x1)>f(x2),
∴f(x)是[0,+∞)上的单调减函数;
(3)根据f(x)是R上的偶函数,且在[0,+∞)上的单调减函数;
∴不等式f(1-t)<f(t)可化为|1-t|>|t|,
即(1-t)2>t2,
解得t<$\frac{1}{2}$,
∴t的取值范围是t<$\frac{1}{2}$.
点评 本题考查了函数的奇偶性与单调性的判断与应用问题,也考查了不等式的解法与应用问题,是综合题目.


科目:高中数学 来源: 题型:选择题
| A. | 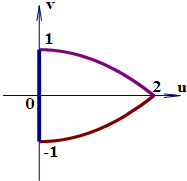 | B. | 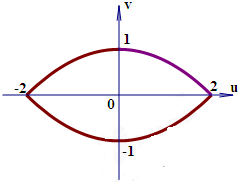 | ||
| C. | 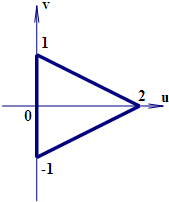 | D. | 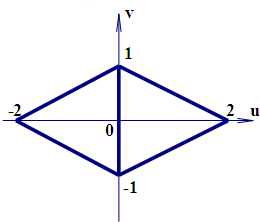 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{5}-4$,$\sqrt{5}+4$] | B. | (-∞,-5] | C. | [-5,+∞) | D. | (-∞,-5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,1] | B. | [$\frac{1}{3}$,1] | C. | [$\frac{1}{4}$,1] | D. | [$\frac{1}{3}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤4} | B. | {x|4<x<11} | C. | {x|1<x<4} | D. | {x|-2≤x<4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com