
【题目】已知函数![]() (k为常数)是实数集R上的奇函数,其中e为自然对数的底数。
(k为常数)是实数集R上的奇函数,其中e为自然对数的底数。
(1)求k的值;
(2)讨论关于x的方程如![]() 的根的个数。
的根的个数。
【答案】(1)k=0,(2)见解析
【解析】
(1)因为定义域是实数集R,直接利用奇函数定义域内有0,则f(﹣0)=﹣f(0)即f(0)=0,即可求k的值;
(2)先把方程转化为![]() x2﹣2ex+m,令F(x)
x2﹣2ex+m,令F(x)![]() (x>0),G(x)=x2﹣2ex+m (x>0),再利用导函数分别求出两个函数的单调区间,进而得到两个函数的最值,比较其最值即可得出结论.
(x>0),G(x)=x2﹣2ex+m (x>0),再利用导函数分别求出两个函数的单调区间,进而得到两个函数的最值,比较其最值即可得出结论.
(1)因为函数f(x)=![]() (k为常数)是实数集R上的奇函数,
(k为常数)是实数集R上的奇函数,
所以f(﹣0)=﹣f(0)即f(0)=0,
则ln(e0+k)=0解得k=0,
显然k=0时,f(x)=x是实数集R上的奇函数;
(2)由(1)得f(x)=x
∴方程转化为![]() x2﹣2ex+m,令F(x)
x2﹣2ex+m,令F(x)![]() (x>0),G(x)=x2﹣2ex+m (x>0),
(x>0),G(x)=x2﹣2ex+m (x>0),
∵F'(x)![]() ,令F'(x)=0,即
,令F'(x)=0,即![]() 0,得x=e
0,得x=e
当x∈(0,e)时,F'(x)>0,∴F(x)在(0,e)上为增函数;
当x∈(e,+∞)时,F'(x)<0,F(x)在(e,+∞)上为减函数;
当x=e时,F(x)max=F(e)![]()
而G(x)=(x﹣e)2+m﹣e2 (x>0)
∴G(x)在(0,e)上为减函数,在(e,+∞)上为增函数;
当x=e时,G(x)min=m﹣e2
∴当m![]() ,即m
,即m![]() 时,方程无解;
时,方程无解;
当m![]() ,即m
,即m![]() 时,方程有一个根;
时,方程有一个根;
当m![]() ,即m
,即m![]() 时,方程有两个根;
时,方程有两个根;


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某学校为了教职工的住房问题,计划征用一块土地盖一幢总建筑面积为![]() 的宿舍楼(每层的建筑面积相同).已知土地的征用费为
的宿舍楼(每层的建筑面积相同).已知土地的征用费为![]() 元
元![]() ,土地的征用面积为第一层的
,土地的征用面积为第一层的![]() 倍,经工程技术人员核算,第一层的建筑费用相同都为400元
倍,经工程技术人员核算,第一层的建筑费用相同都为400元![]() ,以后每增高一层,其建筑费用就增加50元
,以后每增高一层,其建筑费用就增加50元![]() .试设计这幢宿舍楼的楼高层数,使总费用最少,并求出其最少费用.(总费用为建筑费用和征地费用之和).
.试设计这幢宿舍楼的楼高层数,使总费用最少,并求出其最少费用.(总费用为建筑费用和征地费用之和).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数![]() ,使得数列
,使得数列![]() 满足:若
满足:若![]() 是数列
是数列![]() 中的一项,则
中的一项,则![]() 也是数列
也是数列![]() 中的一项,称数列
中的一项,称数列![]() 为“兑换数列”,常数
为“兑换数列”,常数![]() 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列:![]()
![]() 是“兑换系数”为
是“兑换系数”为![]() 的“兑换数列”,求
的“兑换数列”,求![]() 和
和![]() 的值;
的值;
(2)已知有穷等差数列![]() 的项数是
的项数是![]()
![]() ,所有项之和是
,所有项之和是![]() ,求证:数列
,求证:数列![]() 是“兑换数列”,并用
是“兑换数列”,并用![]() 和
和![]() 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不小于3项,且各项皆为正整数的递增数列![]() ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
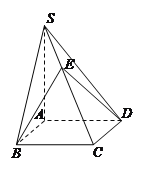
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
(2)排成前后两排,前排4人,后排3人;
(3)全体排成一排,甲不站排头也不站排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥PABCD中,AD∥BC,平面PAC⊥平面ABCD,AB=AD=DC=1,
∠ABC=∠DCB=60,E是PC上一点.
(Ⅰ)证明:平面EAB⊥平面PAC;
(Ⅱ)若△PAC是正三角形,且E是PC中点,求三棱锥AEBC的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com