
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
分析 根据题意画出图形,结合图形用向量$\overrightarrow{AB}$、$\overrightarrow{AC}$表示出$\overrightarrow{AN}$即可.
解答 解:如图所示,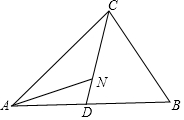
△ABC中,点D为AB边的中点,∴$\overrightarrow{CD}$=$\overrightarrow{AD}$-$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AC}$;
又点N在线段CD上,且$\overrightarrow{CN}$=2$\overrightarrow{ND}$,
∴$\overrightarrow{CN}$=$\frac{2}{3}$$\overrightarrow{CD}$=$\frac{2}{3}$×($\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AC}$)=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$;
∴$\overrightarrow{AN}$=$\overrightarrow{CN}$-$\overrightarrow{CA}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$+$\overrightarrow{AC}$=$\frac{1}{3}$$\overrightarrow{AC}$+$\frac{1}{3}$$\overrightarrow{AB}$,
又$\overrightarrow{AN}$=$\frac{1}{3}$$\overrightarrow{AC}$+λ$\overrightarrow{AB}$,
∴λ=$\frac{1}{3}$.
故选:A.
点评 本题考查了平面向量的线性表示以及平面向量基本定理的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0,-4 | B. | $\frac{4}{27}$,-4 | C. | $\frac{4}{27}$,0 | D. | 2,0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | c>a>b | C. | a>c>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
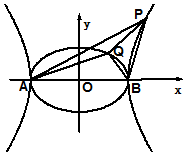 已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点,P、Q分别为双曲线和椭圆上不同于两点A、B的动点,且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ($\overrightarrow{OA}$+$\overrightarrow{QB}$)(λ∈R,|λ|>1),设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,则k1+k2+k3+k4的值( )
已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点,P、Q分别为双曲线和椭圆上不同于两点A、B的动点,且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ($\overrightarrow{OA}$+$\overrightarrow{QB}$)(λ∈R,|λ|>1),设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,则k1+k2+k3+k4的值( )| A. | 大于0 | B. | 等于0 | ||
| C. | 小于0 | D. | 大于0,等于0,小于0都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com