
【题目】如图,四棱锥![]() 中,
中, ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.

(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)当四面体![]() 的体积最大时,判断直线
的体积最大时,判断直线![]() 与直线
与直线![]() 是否垂直,并说明理由.
是否垂直,并说明理由.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】试题分析:(1)取线段![]() 的中点
的中点![]() ,利用平几知识得四边形
,利用平几知识得四边形![]() 是平行四边形,得
是平行四边形,得![]() ,再根据线面平行判定定理得结论,(2)先根据等腰三角形性质得
,再根据线面平行判定定理得结论,(2)先根据等腰三角形性质得![]() .再根据线面垂直性质得
.再根据线面垂直性质得![]() ,由线面垂直判定定理得
,由线面垂直判定定理得![]() 平面
平面![]() .即得
.即得![]() 平面
平面![]() .最后根据面面垂直判定定理得结论,(3)先根据体积公式得
.最后根据面面垂直判定定理得结论,(3)先根据体积公式得![]() 时体积最大.再根据线面垂直得
时体积最大.再根据线面垂直得![]() . 由线面垂直判定定理得
. 由线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]()
试题解析:

(1)证明:取线段![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() 为棱
为棱![]() 的中点,
的中点,
所以在![]() 中
中![]() ,
, ![]() .
.
又![]() ,
, ![]() ,所以
,所以![]() .
.
所以四边形![]() 是平行四边形, 所以
是平行四边形, 所以![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因为![]() ,
, ![]() 为
为![]() 中点,所以
中点,所以![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]()
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(3)![]() .
.
设![]() ,
, ![]()
则四面体![]() 的体积
的体积 ![]()
![]() .
.
当![]() ,即
,即![]() 时体积最大.
时体积最大.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,且离心率为
,且离心率为![]() ,
, ![]() 为椭圆上任意一点,当
为椭圆上任意一点,当![]() 时,
时, ![]() 的面积为1.
的面积为1.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() 是椭圆
是椭圆![]() 上异于椭圆顶点的一点,延长直线
上异于椭圆顶点的一点,延长直线![]() ,
, ![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,
, ![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设![]() 由题
由题 ,由此求出
,由此求出![]() ,可得椭圆
,可得椭圆![]() 的方程;
的方程;
(2)设![]() ,
, ![]() ,
,
当直线![]() 的斜率不存在时,可得
的斜率不存在时,可得![]() ;
;
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,则由
,则由 消去
消去![]() 通过运算可得
通过运算可得
 ,同理可得
,同理可得 ,由此得到直线
,由此得到直线![]() 的斜率为
的斜率为![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,进而可得
,进而可得![]() .
.
试题解析:(1)设![]() 由题
由题 ,
,
解得![]() ,则
,则![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,
,
当直线![]() 的斜率不存在时,设
的斜率不存在时,设 ,则
,则 ,
,
直线![]() 的方程为
的方程为![]() 代入
代入![]() ,可得
,可得![]() ,
,
![]() ,
, ![]() ,则
,则 ,
,
![]() 直线
直线![]() 的斜率为
的斜率为 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
 ,
,
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,则由
,则由 消去
消去![]() 可得:
可得:
![]() ,
,
又![]() ,则
,则![]() ,代入上述方程可得
,代入上述方程可得
![]() ,
,
![]() ,则
,则![]()
 ,
,
设直线![]() 的方程为
的方程为![]() ,同理可得
,同理可得 ,
,
![]() 直线
直线![]() 的斜率为
的斜率为 ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,
![]()
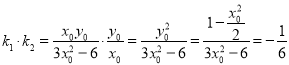 .
.
所以,直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ,即
,即![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,
, ![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击运动员进行射击训练,前三次射击在靶上的着弹点![]() 刚好是边长为
刚好是边长为![]() 的等边三角形的三个顶点.
的等边三角形的三个顶点.

(Ⅰ)第四次射击时,该运动员瞄准![]() 区域射击(不会打到
区域射击(不会打到![]() 外),则此次射击的着弹点距
外),则此次射击的着弹点距![]() 的距离都超过
的距离都超过![]() 的概率为多少?(弹孔大小忽略不计)
的概率为多少?(弹孔大小忽略不计)
(Ⅱ) 该运动员前三次射击的成绩(环数)都在区间![]() 内,调整一下后,又连打三枪,其成绩(环数)都在区间
内,调整一下后,又连打三枪,其成绩(环数)都在区间![]() 内.现从这
内.现从这![]() 次射击成绩中随机抽取两次射击的成绩(记为
次射击成绩中随机抽取两次射击的成绩(记为![]() 和
和![]() )进行技术分析.求事件“
)进行技术分析.求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 左焦点的直线
左焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 过坐标原点且直线
过坐标原点且直线![]() 与
与![]() 的斜率互为相反数,直线
的斜率互为相反数,直线![]() 与椭圆交于
与椭圆交于![]() 两点且均不与点
两点且均不与点![]() 重合,设直线
重合,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .证明:
.证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的半径为2,圆心在
的半径为2,圆心在![]() 轴的正半轴上,且与直线
轴的正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程。
的方程。
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且△
,且△![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的△
的坐标及对应的△![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了配合新冠疫情防控,某市组织了以“停课不停学,成长不停歇”为主题的“空中课堂”,为了了解一周内学生的线上学习情况,从该市中抽取1000名学生进行调査,根据所得信息制作了如图所示的频率分布直方图.

(1)为了估计从该市任意抽取的3名同学中恰有2人线上学习时间在[200,300)的概率![]() ,特设计如下随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,依次用0,1,2,3,…9的前若干个数字表示线上学习时间在[200,300)的同学,剩余的数字表示线上学习时间不在[200,300)的同学;再以每三个随机数为一组,代表线上学习的情况.
,特设计如下随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,依次用0,1,2,3,…9的前若干个数字表示线上学习时间在[200,300)的同学,剩余的数字表示线上学习时间不在[200,300)的同学;再以每三个随机数为一组,代表线上学习的情况.
假设用上述随机模拟方法已产生了表中的30组随机数,请根据这批随机数估计概率![]() 的值;
的值;
907 966 191 925 271 569 812 458 932 683 431 257 027 556
438 873 730 113 669 206 232 433 474 537 679 138 602 231
(2)为了进一步进行调查,用分层抽样的方法从这1000名学生中抽出20名同学,在抽取的20人中,再从线上学习时间[350,450)(350分钟至450分钟之间)的同学中任意选择两名,求这两名同学来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,若函数
,若函数![]() 有三个不同的零点
有三个不同的零点![]() ,
,![]() ,
,![]() (其中
(其中![]() ),则
),则![]() 的取值范围为__________.
的取值范围为__________.
【答案】![]()
【解析】如图:

![]() ,
,![]() ,作出函数图象如图所示
,作出函数图象如图所示
![]() ,
,![]() ,作出函数图象如图所示
,作出函数图象如图所示
![]()
![]() ,由
,由![]() 有三个不同的零点
有三个不同的零点
![]() ,如图
,如图
令![]()
![]()
得![]()
![]()
为满足有三个零点,如图可得
![]() ,
,![]()
![]()
![]()
点睛:本题考查了函数零点问题,先由导数求出两个函数的单调性,继而画出函数图像,再由函数的零点个数确定参量取值范围,将问题转化为函数的两根问题来求解,本题需要化归转化,函数的思想,零点问题等较为综合,有很大难度。
【题型】填空题
【结束】
17
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足:对于任意实数
满足:对于任意实数![]() 都有
都有![]() 恒成立,且当
恒成立,且当![]() 时,
时,![]() .
.
(Ⅰ)判定函数![]() 的单调性,并加以证明;
的单调性,并加以证明;
(Ⅱ)设 ,若函数
,若函数![]() 有三个零点从小到大分别为
有三个零点从小到大分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com