
【题目】设![]() 是一个
是一个![]() 的方格表,在每一个小方格内各填一个正整数.若
的方格表,在每一个小方格内各填一个正整数.若![]() 中的一个
中的一个![]() 方格表的所有数的和为10的倍数,则称其为“好矩形”;若
方格表的所有数的和为10的倍数,则称其为“好矩形”;若![]() 中的一个
中的一个![]() 的小方格不包含于任何一个好矩形,则称其为“坏格”.求
的小方格不包含于任何一个好矩形,则称其为“坏格”.求![]() 中坏格个数的最大值.
中坏格个数的最大值.
【答案】25
【解析】
首先用反证法证明:![]() 中坏格不多于25个.
中坏格不多于25个.
假设结论不成立.则方格表![]() 中至多有1个小方格不是坏格.由表格的对称性,不妨假设此时第1行都是坏格.
中至多有1个小方格不是坏格.由表格的对称性,不妨假设此时第1行都是坏格.
设方格表![]() 第
第![]() 列从上到下填的数依次为
列从上到下填的数依次为![]() 、
、![]() 、
、![]() .
.
记![]() ,
,![]() ,其中,
,其中,![]() .
.
下面证明:三组数![]() ;
;![]() 及
及![]() 都是模10的完全剩余系.
都是模10的完全剩余系.
事实上,假如存在![]() 、
、![]() ,使
,使![]() .则
.则![]() ,即第1行的第
,即第1行的第![]() 列至第
列至第![]() 列组成一个好矩形,与第1行都是坏格矛盾.
列组成一个好矩形,与第1行都是坏格矛盾.
又假如存在![]() 、
、![]() ,使
,使![]() .则
.则![]() ,即第2行至第3行、第
,即第2行至第3行、第![]() 列至第
列至第![]() 列组成一个好矩形.
列组成一个好矩形.
从而,至少有2个小方格不是坏格,矛盾.
类似地,也不存在![]() 、
、![]() ,使
,使![]() .
.
故![]()
![]() .
.
则![]() ,矛盾.
,矛盾.
于是,假设不成立,即坏格不可能多于25个.
其次构造如下一个![]() 的方格表(表1),可验证每个不填10的小方格都是坏格.此时,有25个坏格.
的方格表(表1),可验证每个不填10的小方格都是坏格.此时,有25个坏格.
表 1
1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 10 |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 1 | 1 | 10 | 1 | 1 | 1 | 1 | 2 |
综上,坏格个数的最大值是25.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:

表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:
![]()
如果把5根算筹以适当的方式全部放入 下面的表格中,那么可以表示的三位数的个数为( )
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,在高三年级中随机选取![]() 名学生进行跟踪问卷,其中每周线上学习数学时间不少于
名学生进行跟踪问卷,其中每周线上学习数学时间不少于![]() 小时的有
小时的有![]() 人,在这
人,在这![]() 人中分数不足
人中分数不足![]() 分的有
分的有![]() 人;在每周线上学习数学时间不足于
人;在每周线上学习数学时间不足于![]() 小时的人中,在检测考试中数学平均成绩不足
小时的人中,在检测考试中数学平均成绩不足![]() 分的占
分的占![]() .
.
(1)请完成![]() 列联表;并判断是否有
列联表;并判断是否有![]() 的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
分数不少于 | 分数不足 | 合计 | |
线上学习时间不少于 | |||
线上学习时间不足 | |||
合计 |
(2)在上述样本中从分数不足于![]() 分的学生中,按照分层抽样的方法,抽到线上学习时间不少于
分的学生中,按照分层抽样的方法,抽到线上学习时间不少于![]() 小时和线上学习时间不足
小时和线上学习时间不足![]() 小时的学生共
小时的学生共![]() 名,若在这
名,若在这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求这
人,求这![]() 人每周线上学习时间都不足
人每周线上学习时间都不足![]() 小时的概率.(临界值表仅供参考)
小时的概率.(临界值表仅供参考)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式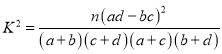 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拿破仑为人好学,是法兰西科学院院士,他对数学方面很感兴趣,在行军打仗的空闲时间,经常研究平面几何。他提出了著名的拿破仑定理:以三角形各边为边分别向外(内)侧作等边三角形,则它们的中心构成一个等边三角形。如图所示,以等边![]() 的三条边为边,向外作
的三条边为边,向外作![]() 个正三角形,取它们的中心
个正三角形,取它们的中心![]() ,顺次连接,得到
,顺次连接,得到![]() ,图中阴影部分为
,图中阴影部分为![]() 与
与![]() 的公共部分。若往
的公共部分。若往![]() 中投掷一点,则该点落在阴影部分内的概率为( )
中投掷一点,则该点落在阴影部分内的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() 与圆
与圆![]() 相交的弦长等于椭圆
相交的弦长等于椭圆![]() :
: ![]() (
(![]() )的焦距长.
)的焦距长.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,椭圆
为原点,椭圆![]() 与抛物线
与抛物线![]() (
(![]() )交于
)交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一动点,若直线
上一动点,若直线![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某外卖企业两位员工今年![]() 月某
月某![]() 天日派送外卖量的数据(单位:件),如茎叶图所示针对这
天日派送外卖量的数据(单位:件),如茎叶图所示针对这![]() 天的数据,下面说法错误的是( )
天的数据,下面说法错误的是( )
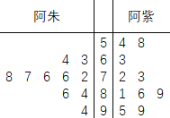
A.阿朱的日派送量的众数为![]() B.阿紫的日派送量的中位数为
B.阿紫的日派送量的中位数为![]()
C.阿朱的日派送量的中位数为![]() D.阿朱的日派送外卖量更稳定
D.阿朱的日派送外卖量更稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com