
【题目】兰州一中在世界读书日期间开展了“书香校园”系列读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”。
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 |
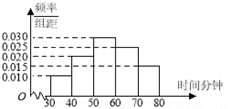
(1)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(2)利用分层抽样从这100名学生的“读书迷”中抽取8名进行集训,从中选派2名参加兰州市读书知识比赛,求至少有一名男生参加比赛的概率。
附: 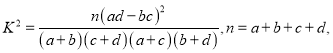
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【答案】(1)表格见解析, 有99%的把握认为“读书迷”与性别有关;(2) ![]()
【解析】试题分析:(1)根据题意完成列联表即可,再利用所给公式和临界值表进行判定;(2)先利用分层抽样确定人数,再利用古典概型的概率公式进行求解.
试题解析:(1)2×2列联表如下:
非读书迷 | 读书迷” | 合计 | |
男 | 40 | 15 | 55 |
女 | 20 | 25 | 45 |
合计 | 60 | 40 | 100 |
易知![]() 的观测值
的观测值![]()
因为![]() ,所以有99%的把握认为“读书迷”与性别有关.
,所以有99%的把握认为“读书迷”与性别有关.
(2)利用分层抽样抽取的8名“读书迷”中有男生3名,女生5名,分别设男生和女生为![]() 、
、![]() , 设从8名“读书迷”中选派2名,至少选派一名男生参加比赛的事件为
, 设从8名“读书迷”中选派2名,至少选派一名男生参加比赛的事件为![]() 则基本事件共有28种,其中至少选派一名男生参加比赛的事件有18种,
则基本事件共有28种,其中至少选派一名男生参加比赛的事件有18种,
所以, ![]() 所以,至少有一名男生参加比赛的概率为
所以,至少有一名男生参加比赛的概率为![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0, ![]() )的部分图象如图所示.
)的部分图象如图所示. 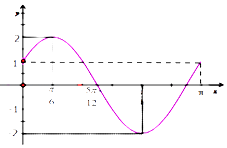
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间和对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某刻考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差![]() (单位:分)与物理偏差
(单位:分)与物理偏差![]() (单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:
(单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:

(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若这次考试该班数学平均分为120分,物理平均分为92,试预测数学成绩126分的同学的物理成绩.
参考公式:  ,
, ![]()
参考数据: ![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下![]() 的列联表:
的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确的是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的函数 ![]() .
.
(1)如果函数 ![]() ,求b、c;
,求b、c;
(2)设当x∈( ![]() ,3)时,函数y=f(x)﹣c(x+b)的图象上任一点P处的切线斜率为k,若k≤2,求实数b的取值范围.
,3)时,函数y=f(x)﹣c(x+b)的图象上任一点P处的切线斜率为k,若k≤2,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N分别是BC1 , CD1的中点,则下列说法错误的是( ) 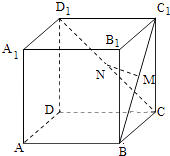
A.MN与CC1垂直
B.MN与AC垂直
C.MN与BD平行
D.MN与A1B1平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),函数f(x)=
),函数f(x)= ![]()
![]() ﹣m|
﹣m| ![]() +
+ ![]() |+1,x∈[﹣
|+1,x∈[﹣ ![]() ,
, ![]() ],m∈R.
],m∈R.
(1)当m=0时,求f( ![]() )的值;
)的值;
(2)若f(x)的最小值为﹣1,求实数m的值;
(3)是否存在实数m,使函数g(x)=f(x)+ ![]() m2 , x∈[﹣
m2 , x∈[﹣ ![]() ,
, ![]() ]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com