4π 3

(0,2)
分析:(A)通过弦切角转化为,圆周角,然后求出圆心角,结合弦长,得到半径,然后求出圆的面积.
(B)把极坐标方程化为直角坐标方程,求出圆心到直线的距离,再由弦长公式求出弦长.
(C)由不等式可得①

,或②

,或 ③

.分别求出①②③的解集,再取并集即可求得不等式的解集.
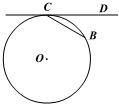
解答:(A)因为弦切角等于同弧上的圆周角,

所以,∠BCD=30°,
∠A=30°,则∠BOC=60°,
根据60°的圆心角所对弦等于半径,BC=2,
所以圆的半径为2,所以圆的面积为:4π
故答案为:4π.
(B)极坐标方程ρ=2sinθ+4cosθ 化为直角坐标方程为
(x-2)
2+(y-1)
2=5,
表示的曲线是以(2,1)为圆心,以

为半径的圆.
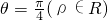
化为直角坐标方程为 y=x,表示一条直线.
圆心到直线的距离等于d=
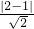
=

.
∴方程ρ=2sinθ+4cosθ表示的曲线截
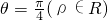
所得的弦长为 2

=2

=3

,
故答案为 3

.
(C)由不等式|2x-1|<|x|+1即|2x-1|-|x|<1,可得①

,或②

,或 ③

.
解①得x∈∅,解②得 0<x<

,解③得

≤x<2.
综上可得,不等式的解集为 (0,2),
故答案为 (0,2).
点评:本题主要考查弦切角的应用,圆周角与圆心角的关系,确定面积的求法;把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,绝对值不等式的求法,考查计算能力,
属于中档题.

 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)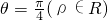 所得的弦长为________;
所得的弦长为________; (0,2)
(0,2) ,或②
,或② ,或 ③
,或 ③ .分别求出①②③的解集,再取并集即可求得不等式的解集.
.分别求出①②③的解集,再取并集即可求得不等式的解集. 所以,∠BCD=30°,
所以,∠BCD=30°, 为半径的圆.
为半径的圆.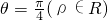 化为直角坐标方程为 y=x,表示一条直线.
化为直角坐标方程为 y=x,表示一条直线.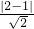 =
= .
.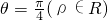 所得的弦长为 2
所得的弦长为 2 =2
=2 =3
=3 ,
, .
. ,或②
,或② ,或 ③
,或 ③ .
. ,解③得
,解③得 ≤x<2.
≤x<2.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)