
【题目】【南京市、盐城市2017届高三年级第二次模拟】(本小题满分14分)
在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.

【答案】见解析
【解析】(1)因为矩形纸板ABCD的面积为3600,故当a=90时,b=40,
从而包装盒子的侧面积
S=2×x(90-2x)+2×x(40-2x)
=-8x2+260x,x∈(0,20).…………………3分
因为S=-8x2+260x=-8(x-)2+,
故当x=时,侧面积最大,最大值为平方厘米.
答:当x=时,纸盒的侧面积的最大值为平方厘米.…………………6分
(2)包装盒子的体积
V=(a-2x)(b-2x)x=x[ab-2(a+b)x+4x2],x∈(0,),b≤60.……………8分
V=x[ab-2(a+b)x+4x2]≤x(ab-4x+4x2)
=x(3600-240x+4x2)
=4x3-240x2+3600x.…………………10分
当且仅当a=b=60时等号成立.
设f(x)=4x3-240x2+3600x,x∈(0,30).
则f′(x)=12(x-10)(x-30).
于是当0<x<10时,f′(x)>0,所以f(x)在(0,10)上单调递增;
当10<x<30时,f′(x)<0,所以f(x)在(10,30)上单调递减.
因此当x=10时,f(x)有最大值f(10)=16000,………………12分
此时a=b=60,x=10.
答:当a=b=60,x=10时纸盒的体积最大,最大值为16000立方厘米.
………………14分


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】将函数h(x)=2sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象( )
个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象( )
A.关于直线x=0对称
B.关于直线x=π对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,2)对称
,2)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016-2017学年度苏锡常镇四市高三教学情况调研(二)】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
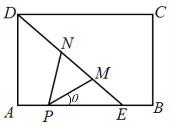
【题目】【2017扬州一模】如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在![]() ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,
ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,![]() 为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,
为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() PMN的面积为S平方米.
PMN的面积为S平方米.
(1)求S关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017重庆市八中5月模考】已知![]() (
(![]() ),
),![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)若在(1)的条件下,当![]() 取最大值时,求证:
取最大值时,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成的角为( )
A.90°
B.45°
C.60°
D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com