
【题目】如图所示,有![]() 、
、![]() 、
、![]() 三座城市,
三座城市,![]() 城在
城在![]() 城的正西方向,且两座城市之间的距离为
城的正西方向,且两座城市之间的距离为![]() ;
;![]() 城在
城在![]() 城的正北方向,且两座城市之间的距离为
城的正北方向,且两座城市之间的距离为![]() .由
.由![]() 城到
城到![]() 城只有一条公路
城只有一条公路![]() ,甲有急事要从
,甲有急事要从![]() 城赶到
城赶到![]() 城,现甲先从
城,现甲先从![]() 城沿公路
城沿公路![]() 步行到点
步行到点![]() (不包括
(不包括![]() 、
、![]() 两点)处,然后从点
两点)处,然后从点![]() 处开始沿山路
处开始沿山路![]() 赶往
赶往![]() 城.若甲在公路上步行速度为每小时
城.若甲在公路上步行速度为每小时![]() ,在山路上步行速度为每小时
,在山路上步行速度为每小时![]() ,设
,设![]() (单位:弧度),甲从
(单位:弧度),甲从![]() 城赶往
城赶往![]() 城所花的时间为
城所花的时间为![]() (单位:
(单位:![]() ).
).

(1)求函数![]() 的表达式,并求函数的定义域;
的表达式,并求函数的定义域;
(2)当点![]() 在公路
在公路![]() 上何处时,甲从
上何处时,甲从![]() 城到达
城到达![]() 城所花的时间最少,并求所花的最少的时间的值.
城所花的时间最少,并求所花的最少的时间的值.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项为1,且
的首项为1,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,对任意
,对任意![]() ,都有
,都有![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
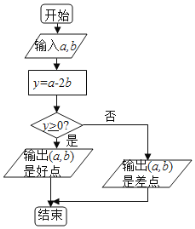
【题目】执行如图所示的程序框图后,记“输出![]() 是好点”为事件A.
是好点”为事件A.
(1)若![]() 为区间
为区间![]() 内的整数值随机数,
内的整数值随机数,![]() 为区间
为区间![]() 内的整数值随机数,求事件A发生的概率;
内的整数值随机数,求事件A发生的概率;
(2)若![]() 为区间
为区间![]() 内的均匀随机数,
内的均匀随机数,![]() 为区间
为区间![]() 内的均匀随机数,求事件A发生的概率.
内的均匀随机数,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ ![]() x2﹣ax(a为常数)有两个极值点.
x2﹣ax(a为常数)有两个极值点.
(1)求实数a的取值范围;
(2)设f(x)的两个极值点分别为x1 , x2 , 若不等式f(x1)+f(x2)<λ(x1+x2)恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要想得到函数y=sin2x+1的图象,只需将函数y=cos2x的图象( )
A.向左平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
B.向右平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
C.向左平移 ![]() 个单位,再向下平移1个单位
个单位,再向下平移1个单位
D.向右平移 ![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的最大值;
的最大值;
(2)若对于任意![]() ,均有
,均有![]() ,求正实数
,求正实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得不等式
,使得不等式![]() 对于任意
对于任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-1|+|x-2|.
(1)求不等式f(x)≥3的解集;
(2)若存在实数x满足f(x)≤-a2+a+7,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com