
【题目】已知函数f(x)=2sin ![]() cos
cos ![]() ﹣2
﹣2 ![]() sin2
sin2 ![]() +
+ ![]()
(1)求函数f(x)的单调减区间
(2)已知α∈( ![]() ,
, ![]() ),且f(α)=
),且f(α)= ![]() ,求f(
,求f( ![]() )的值.
)的值.
【答案】
(1)解:化简可得f(x)=2sin ![]() cos
cos ![]() ﹣2
﹣2 ![]() sin2
sin2 ![]() +
+ ![]()
=sinx+ ![]() cosx=2sin(x+
cosx=2sin(x+ ![]() ),
),
由2kπ+ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() 可得2kπ+
可得2kπ+ ![]() ≤x≤2kπ+
≤x≤2kπ+ ![]() ,
,
∴函数f(x)的单调减区间为:[2kπ+ ![]() ,2kπ+
,2kπ+ ![]() ](k∈Z)
](k∈Z)
(2)解:∵α∈( ![]() ,
, ![]() ),且f(α)=2sin(α+
),且f(α)=2sin(α+ ![]() )=
)= ![]() ,
,
∴sin(α+ ![]() )=
)= ![]() ,∴cos(α+
,∴cos(α+ ![]() )=﹣
)=﹣ ![]()
∴f( ![]() )=2sin(α﹣
)=2sin(α﹣ ![]() +
+ ![]() )=2sin(α+
)=2sin(α+ ![]() ﹣
﹣ ![]() )
)
=2sin(α+ ![]() )cos
)cos ![]() ﹣2cos(α+
﹣2cos(α+ ![]() )sin
)sin ![]()
=2× ![]() ﹣2×
﹣2× ![]() =
= ![]()
【解析】(1)化简可得f(x)=2sin(x+ ![]() ),解不等式2kπ+
),解不等式2kπ+ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() 可得单调减区间;(2)由题意易得sin(α+
可得单调减区间;(2)由题意易得sin(α+ ![]() )=
)= ![]() ,∴cos(α+
,∴cos(α+ ![]() )=﹣
)=﹣ ![]() ,而f(
,而f( ![]() )=2sin(α+
)=2sin(α+ ![]() )cos
)cos ![]() ﹣2cos(α+
﹣2cos(α+ ![]() )sin
)sin ![]() ,代值计算可得.
,代值计算可得.
【考点精析】关于本题考查的两角和与差的正弦公式,需要了解两角和与差的正弦公式:![]() 才能得出正确答案.
才能得出正确答案.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
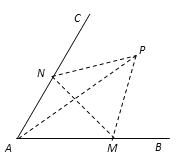
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与
与![]() (
(![]() 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为![]() .若动点
.若动点![]() 满足
满足![]() ,试探究是否存在两个定点
,试探究是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年春节,“抢红包”成为社会热议的话题之一.某机构对春节期间用户利用手机“抢红包”的情况进行调查,如果一天内抢红包的总次数超过10次为“关注点高”,否则为“关注点低”,调查情况如下表所示:
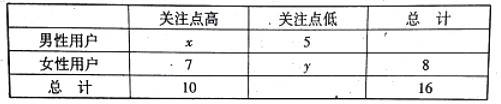
(1)填写上表中x,y的值并判断是否有95%以上的把握认为性别与关注点高低有关?
(2)现要从上述男性用户中随机选出3名参加一项活动,以X表示选中的同学中抢红包总次数超过10次的人数,求随机变量X的分布列及数学期望E(X).
下面的临界值表供参考:

独立性检验统计量 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com