【题目】己知直线2x+y﹣8=0与直线x﹣2y+1=0交于点P．
（1）求过点P且平行于直线4x﹣3y﹣7=0的直线11的方程；（结果都写成一般方程形式）
（2）求过点P的所有直线中使原点O到此直线的距离最大的直线12的方程．
【答案】
（1）解：由 
，解得x=3，y=2，
∴直线2x+y﹣8=0与直线x﹣2y+1=0的交点P（3，2），
∵过点P且平行于直线4x﹣3y﹣7=0的直线11的斜率k1= 
，
∴直线l1的方程为y﹣2= （x﹣3），
∴过点P且平行于直线4x﹣3y﹣7=0的直线11的方程为4x﹣3y﹣6=0
（2）解：当OP⊥l2时，原点O到此直线的距离最大，
又kOP= 
时，则直线l2的斜率k2=﹣ 
，
∴直线l2的方程为y﹣2=﹣ （x﹣3），即3x+2y﹣13=0
【解析】（1）先求出直线2x+y﹣8=0与直线x﹣2y+1=0的交点P，再由直线与直线平行的关系能求出过点P且平行于直线4x﹣3y﹣7=0的直线11的方程．（2）当OP⊥l2时，原点O到此直线的距离最大，由此能求出直线l2的方程．
小夫子全能检测系列答案科目：高中数学 来源： 题型：
【题目】已知曲线
为参数），
为参数）.
（1）化
的参数方程为普通方程，并说明它们分别表示什么曲线；
（2）若
上的点
对应的参数为
为
上的动点，求
的中点
到直线
为参数）距离的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
=1（a＞b＞0）过点A（2，0），B（0，1）两点．
（1）求椭圆C的方程及离心率；
（2）设直线l与椭圆相交于不同的两点A，B．已知点A的坐标为（﹣a，0），点 Q（0，y0）在线段AB的垂直平分线上，且 
=4，求y0的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示的几何体中，四边形AA1B1B是边长为3的正方形，CC1=2，CC1∥AA1 ， 这个几何体是棱柱吗？若是，指出是几棱柱．若不是棱柱，请你试用一个平面截去一部分，使剩余部分是一个棱长为2的三棱柱，并指出截去的几何体的特征，在立体图中画出截面．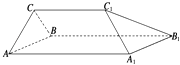 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个透明密闭的正方体容器中，恰好盛有该容器一半容积的水，任意转动这个正方体，则水面在容器中的形状可以是：
①三角形；②矩形；③正方形；④正六边形．
其中正确的结论是（把你认为正确的序号都填上）
查看答案和解析>>
科目：高中数学 来源： 题型：
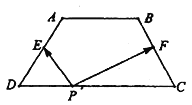
【题目】如图，梯形
中， 
， 
， 
， 
, 
和
分别为
与
的中点，对于常数
，在梯形
的四条边上恰好有8个不同的点
，使得
成立，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，AB是圆O的直径，C是圆O上不同于A，B的一点，PA⊥平面ABC，E是PC的中点， 
，PA=AC=1． 
（1）求证：AE⊥PB；
（2）求二面角A﹣PB﹣C的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图⑴、⑵、⑶、⑷为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为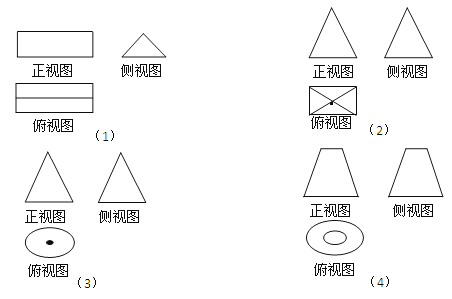
A.三棱台、三棱柱、圆锥、圆台
B.三棱台、三棱锥、圆锥、圆台
C.三棱柱、正四棱锥、圆锥、圆台
D.三棱柱、三棱台、圆锥、圆台
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
