
���� ��1����������˶�û�вμӽ�Ŀ�ĸ��ʣ����ɶ����¼��ĸ��ʹ�ʽ���������λͬѧ��������һλ�μӹ��˽�Ŀ�ĸ��ʣ�
��2���������ͨ��Ԥѡ������X�Ŀ���ȡֵΪ0��1��2��3��4��5���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к���ѧ������
��� �⣺��1������5��ͬѧ�����ѡ��2�ˣ�����${C}_{5}^{2}$=10�������
����5��ͬѧ�����ѡ���ˣ������˶�û�вμӹ��˽�Ŀ�������${C}_{3}^{2}$=3�֣�
������λͬѧ��������һλ�μӹ��˽�Ŀ�ĸ��ʣ�
p=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=0.7��
��2���������ͨ��Ԥѡ������X�Ŀ���ȡֵΪ0��1��2��3��4��5��
P��X=0��=$��\frac{1}{2}��^{2}��\frac{2}{3}��^{3}$=$\frac{8}{108}$��
P��X=1��=��${C}_{2}^{1}��\frac{1}{2}��^{2}��\frac{2}{3}��^{3}+��\frac{1}{2}��^{2}{C}_{3}^{1}��\frac{1}{3}��$$��\frac{2}{3}��^{2}=\frac{28}{108}$��
P��X=2��=${C}_{2}^{2}��\frac{1}{2}��^{2}��\frac{2}{3}��^{3}$+$��\frac{1}{2}��^{2}{C}_{3}^{2}��\frac{1}{2}��^{2}•\frac{2}{3}$+${C}_{2}^{1}��\frac{1}{2}��^{2}{C}_{3}^{1}��\frac{2}{3}��^{3}$$•\frac{1}{3}$=$\frac{38}{108}$��
P��X=3��=${C}_{2}^{2}��\frac{1}{2}��^{2}{C}_{3}^{1}��\frac{2}{3}��^{2}•\frac{1}{3}+{C}_{2}^{1}��\frac{1}{2}��^{2}$$•{C}_{3}^{2}��\frac{1}{3}��^{2}•\frac{2}{3}$+$��\frac{1}{2}��^{2}{C}_{3}^{3}��\frac{1}{3}��^{3}$=$\frac{25}{108}$��
P��X=4��=${C}_{2}^{2}��\frac{1}{2}��^{2}{C}_{3}^{2}��\frac{1}{3}��^{2}+{C}_{2}^{1}��\frac{1}{2}��^{2}$$•{C}_{3}^{3}��\frac{1}{3}��^{3}$=$\frac{8}{108}$��
P��X=5��=${C}_{2}^{2}��\frac{1}{2}��^{2}{C}_{3}^{3}��\frac{1}{3}��^{3}$=$\frac{1}{108}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{8}{108}$ | $\frac{28}{108}$ | $\frac{38}{108}$ | $\frac{25}{108}$ | $\frac{8}{108}$ | $\frac{1}{108}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬������߿��ж��DZؿ�����֮һ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
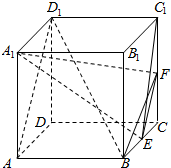 ��֪������ABCD-A1B1C1D1�ĵ����DZ߳�Ϊ2����������AA1�͵���ABCD��AA1=4��EΪBC���е㣬FΪCC1���е㣮
��֪������ABCD-A1B1C1D1�ĵ����DZ߳�Ϊ2����������AA1�͵���ABCD��AA1=4��EΪBC���е㣬FΪCC1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ֧�� | ���� | ��֧�� |
| 450 | 300 | 150 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y2=16x | B�� | y2=-8x | C�� | y2=-16x | D�� | x2=-16y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$i | B�� | $\frac{1}{2}$ | C�� | -$\frac{1}{2}$i | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����֪��V-ABC�ĵ������64cm2��ƽ���ڵ���Ľ��������4cm2��������V�ڽ���͵����ϵ���Ӱ�ֱ���O1��O����O1O�����ȷֵ���ƽ���ڵ���Ľ��棬�������������
��ͼ��ʾ����֪��V-ABC�ĵ������64cm2��ƽ���ڵ���Ľ��������4cm2��������V�ڽ���͵����ϵ���Ӱ�ֱ���O1��O����O1O�����ȷֵ���ƽ���ڵ���Ľ��棬��������������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com