
【题目】已知圆C经过点A(1,1)和B(4,﹣2),且圆心C在直线l:x+y+1=0上.
(Ⅰ)求圆C的标准方程;
(Ⅱ)设M,N为圆C上两点,且M,N关于直线l对称,若以MN为直径的圆经过原点O,求直线MN的方程.
【答案】解:(Ⅰ)∵A(1,1),B(4,﹣2)∴直线AB的斜率 ![]()
∴直线AB的垂直平分线的斜率为1
又线段AB的中点坐标为 ![]()
∴线段AB的垂直平分线的方程是 ![]() ,即x﹣y﹣3=0
,即x﹣y﹣3=0
∵圆心C在直线l:x+y+1=0上
∴圆心C的坐标是方程组 ![]() 的解,得圆心C的坐标(1,﹣2)
的解,得圆心C的坐标(1,﹣2)
∴圆C的半径长 ![]()
∴圆C的标准方程是(x﹣1)2+(y+2)2=9
(Ⅱ)设以MN为直径的圆的圆心为P,半径为r
∵M,N是圆C上的两点,且M,N关于直线l:x+y+1=0对称
∴点P在直线l:x+y+1=0上
∴可以设点P坐标为(m,﹣1﹣m)
∵以MN为直径的圆经过原点O
∴以MN为直径的圆的半径长 ![]()
∵MN是圆C的弦,
∴|CP|2+r2=9,即(m﹣1)2+(m﹣1)2+m2+(m+1)2=9,解得m=﹣1或 ![]()
∴点P坐标为(﹣1,0)或 ![]()
∵直线MN垂直直线l:x+y+1=0,
∴直线MN的斜率为1
∴直线MN的方程为:x﹣y+1=0或x﹣y﹣4=0
【解析】(Ⅰ)根据题意,分析可得圆C的圆心是线段AB的垂直平分线与直线l的交点,先求出线段AB的垂直平分线的方程,与直线l联立可得圆心C的坐标,进而可得圆的半径,即可得答案;(Ⅱ)设以MN为直径的圆的圆心为P,半径为r,可以设p的坐标为(m,﹣1﹣m),结合直线与圆的位置关系可得(m﹣1)2+(m﹣1)2+m2+(m+1)2=9,解得m的值,即可得p的坐标,分析可得直线MN的斜率为1,由直线的点斜式方程可得答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①若![]() ,则
,则![]() ;
;
②若![]() 是不共线的四点,则
是不共线的四点,则![]() 是四边形
是四边形![]() 为平行四边形的充要条件;
为平行四边形的充要条件;
③若![]() ,
, ![]() ,则
,则![]() ;
;
④![]() 的充要条件是
的充要条件是![]() 且
且![]()
其中正确命题的序号是( )
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈(0, ![]() ))的图象在y轴上的截距为1,在相邻两个最值点
))的图象在y轴上的截距为1,在相邻两个最值点 ![]() 和(x0 , ﹣2)上(x0>0),函数f(x)分别取最大值和最小值.
和(x0 , ﹣2)上(x0>0),函数f(x)分别取最大值和最小值.
(1)求函数f(x)的解析式;
(2)若f(x)= ![]() 在区间
在区间 ![]() 内有两个不同的零点,求k的取值范围;
内有两个不同的零点,求k的取值范围;
(3)求函数f(x)在区间 ![]() 上的对称轴方程.
上的对称轴方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinx﹣bcosx(a、b为常数,a≠0,x∈R)在x= ![]() 处取得最小值,则函数y=f(
处取得最小值,则函数y=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函数且它的图象关于点(π,0)对称
B.偶函数且它的图象关于点 ![]() 对称
对称
C.奇函数且它的图象关于点 ![]() 对称
对称
D.奇函数且它的图象关于点(π,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是世界读书日,惠州市某中学在此期间开展了一系列的读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”.
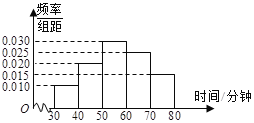
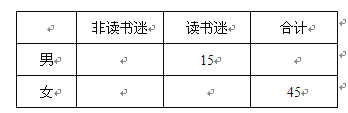
(Ⅰ)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(Ⅱ)将频率视为概率,现在从该校大量学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“读书迷”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和方差
和方差![]() .
.
附: 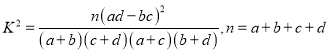
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0 ) 经过点 P(1,
(a>b>0 ) 经过点 P(1, ![]() ),离心率 e=
),离心率 e= ![]()
(Ⅰ)求椭圆C的标准方程.
(Ⅱ)设过点E(0,﹣2 ) 的直线l 与C相交于P,Q两点,求△OPQ 面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com