
【题目】如图,已知椭圆![]() ,过点
,过点![]() ,离心率为
,离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() .点
.点![]() 为直线
为直线![]() 上且不在
上且不在![]() 轴上的任意一点,直线
轴上的任意一点,直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 为坐标原点.
为坐标原点.

(![]() )求椭圆的标准方程;
)求椭圆的标准方程;
(![]() )设直线
)设直线![]() 、
、![]() 斜率分别为
斜率分别为![]() 、
、![]() .
.
①证明:![]() ;
;
②问直线![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率
的斜率![]() 、
、![]() 、
、![]() 、
、![]() 满足
满足![]() ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)①证明见解析,②
;(2)①证明见解析,②![]() .
.
【解析】![]()
试题分析:(1)利用椭圆过已知点和离心率结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求得
的方程组,求得![]() 和
和![]() ,则椭圆的方程可得;(2)①把直线
,则椭圆的方程可得;(2)①把直线![]() 的方程联立求得交点的坐标的表达式,代入直线
的方程联立求得交点的坐标的表达式,代入直线![]() 上,整理求得
上,整理求得![]() ,原式得证;②设出
,原式得证;②设出![]() 的坐标,联立直线
的坐标,联立直线![]() 和椭圆的方程根据韦达定理表示出
和椭圆的方程根据韦达定理表示出![]() 和
和![]() ,进而可求得直线
,进而可求得直线![]() 、
、![]() 斜率的和与
斜率的和与![]() 、
、![]() 斜率的和,由
斜率的和,由![]() ,推断出
,推断出![]() 或
或![]() 分别讨论可求得点
分别讨论可求得点![]() 的坐标.
的坐标.
试题解析:(![]() )因为椭圆过点
)因为椭圆过点![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
又![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
故椭圆方程为![]() .
.
(![]() )①设
)①设![]() ,则
,则![]() ,
,![]() ,
,
因为点![]() 不在
不在![]() 轴上,所以
轴上,所以![]() .
.
又![]() ,
,
所以![]() .
.
②设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立直线![]() 与椭圆方程得
与椭圆方程得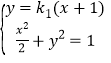 ,
,
化简得![]() ,
,
因此![]() ,
,![]() ,
,
由于![]() 、
、![]() 斜率存在,
斜率存在,
所以![]() ,
,![]() ,因此
,因此![]() ,
,![]() ,
,
因此![]() .
.
类似可以得到
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() .
.
若![]() ,必须有
,必须有![]() 或
或![]() .
.
当![]() 时,结合①的结论,可得
时,结合①的结论,可得![]() ,
,
所以解得![]() 点坐标为
点坐标为![]() .
.
当![]() 时,结合①的结论,可得
时,结合①的结论,可得![]() 或
或![]() (舍去),
(舍去),
此时直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程![]() 得
得![]() ,
,![]() .
.
因此![]() 点坐标为
点坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图是甲、乙两名运动员某赛季一些场次得分的茎叶图,据图可知以下说法正确的是 _____.(填序号)

①甲运动员的成绩好于乙运动员;②乙运动员的成绩好于甲运动员;
③甲、乙两名运动员的成绩没有明显的差异;④甲运动员的最低得分为0分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P-ABC中,PC![]() 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD![]() 平面PAB
平面PAB
(1)求证:AB![]() 平面PCB
平面PCB
(2)求异面直线AP与BC所成角的大小
(3)求二面角C-PA-B 的大小的余弦值

查看答案和解析>>
科目:高中数学 来源: 题型:
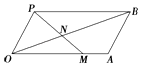
【题目】如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若 ![]() ,
, ![]() .
. 
(1)把y用x表示出来(即求y=f(x)的解析式);
(2)设数列{an}的首项a1=1,前n项和Sn满足Sn=f(Sn﹣1)(n≥2且n∈N*),求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活.—媒体为调查市民对低头族的认识,从某社区的500名市民中随机抽取![]() 名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:


(1)求出表中![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定在第2,4,5组中用分层抽样的方法抽取6名市民进行问卷调查, 再从这6名市民中随机抽取2名接受电视采访,求第2组至少有一名接受电视采访的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海域的东西方向上分别有A,B两个观测点(如图),它们相距![]() 海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距
海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距![]() 海里的C点有一救援船,其航行速度为30海里/小时.
海里的C点有一救援船,其航行速度为30海里/小时.

(1)求B点到D点的距离BD;
(2)若命令C处的救援船立即前往D点营救,求该救援船到达D点需要的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.
(Ⅰ)求{an}的通项公式an与前n项和公式Sn;
(Ⅱ)令bn=![]() (k<0),若{bn}是等差数列,求数列{
(k<0),若{bn}是等差数列,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
(I)求应从这三个协会中分别抽取的运动员人数;
(II)将抽取的6名运动员进行编号,编号分别为![]() ,从这6名运动员中随机抽取2名参加双打比赛.
,从这6名运动员中随机抽取2名参加双打比赛.
(i)用所给编号列出所有可能的结果;
(ii)设A为事件“编号为![]() 的两名运动员至少有一人被抽到”,求事件A发生的概率.
的两名运动员至少有一人被抽到”,求事件A发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com