
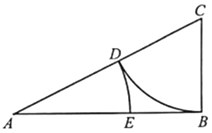
【题目】古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出己知线段的黄金分割点,具体方法如下:(l)取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=![]() AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:
AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:![]() 2.236)
2.236)
A. 0.236B. 0.382C. 0.472D. 0.618
科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱![]() 中,
中,![]() ,
,![]() ,其中
,其中![]() 为棱
为棱![]() 上的中点,
上的中点,![]() 为棱
为棱![]() 上且位于
上且位于![]() 点上方的动点.
点上方的动点.

(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知城市![]() 周边有两个小镇
周边有两个小镇![]() 、
、![]() ,其中乡镇
,其中乡镇![]() 位于城市
位于城市![]() 的正东方
的正东方![]() 处,乡镇
处,乡镇![]() 与城市
与城市![]() 相距
相距![]() ,
,![]() 与
与![]() 夹角的正切值为2,为方便交通,现准备建设一条经过城市
夹角的正切值为2,为方便交通,现准备建设一条经过城市![]() 的公路
的公路![]() ,使乡镇
,使乡镇![]() 和
和![]() 分别位于
分别位于![]() 的两侧,过
的两侧,过![]() 和
和![]() 建设两条垂直
建设两条垂直![]() 的公路
的公路![]() 和
和![]() ,分别与公路
,分别与公路![]() 交汇于
交汇于![]() 、
、![]() 两点,以
两点,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的平面直角坐标系
轴,建立如图所示的平面直角坐标系![]() .
.

(1)当两个交汇点![]() 、
、![]() 重合,试确定此时
重合,试确定此时![]() 路段长度;
路段长度;
(2)当![]() ,计算此时两个交汇点
,计算此时两个交汇点![]() 、
、![]() 到城市
到城市![]() 的距离之比;
的距离之比;
(3)若要求两个交汇点![]() 、
、![]() 的距离不超过
的距离不超过![]() ,求
,求![]() 正切值的取值范围.
正切值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若三次函数![]() (
(![]() )的图象上存在相互平行且距离为
)的图象上存在相互平行且距离为![]() 的两条切线,则称这两条切线为一组“距离为
的两条切线,则称这两条切线为一组“距离为![]() 的友好切线组”.已知
的友好切线组”.已知![]() ,则函数
,则函数![]() 的图象上“距离为4的友好切线组”有( )组?
的图象上“距离为4的友好切线组”有( )组?
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() (
(![]() ).对上述数据作了初步处理,得到相关的值如表:
).对上述数据作了初步处理,得到相关的值如表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() 若想在
若想在![]() 年达到年利润最大,请预测
年达到年利润最大,请预测![]() 年的宣传费用是多少万元?
年的宣传费用是多少万元?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() )作为样本(样本容量为
)作为样本(样本容量为![]() )进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.
)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.

(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)估计本次竞赛学生成绩的中位数;
(3)在选取的样本中,从竞赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生,求所抽取的
名学生,求所抽取的![]() 名学生中至少有一人得分在
名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com