
【题目】已知函数![]() ,其中
,其中![]() 且
且![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若存在
时,若存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() ,
,
当![]() 时,
时,![]() 的减区间是
的减区间是![]() ,增区间是
,增区间是![]() (2)
(2)![]()
【解析】
试题分析:(1)先求函数导数![]() ,根据
,根据![]() 的正负讨论导数符号变化规律,进而得单调区间(2)对应不等式有解问题,一般利用变量分离法,转化为对应函数最值问题:
的正负讨论导数符号变化规律,进而得单调区间(2)对应不等式有解问题,一般利用变量分离法,转化为对应函数最值问题:![]() 最大值,再利用导数求函数
最大值,再利用导数求函数![]() 最大值,先求函数导数
最大值,先求函数导数![]() ,再求导函数零点
,再求导函数零点![]() ,列表分析导函数符号变化规律,进而得出单调性,确定极值与最值
,列表分析导函数符号变化规律,进而得出单调性,确定极值与最值
试题解析:(1)定义域为![]() ,
,![]() ....................... 2分
....................... 2分
当![]() 时,
时,![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 时,
时,![]() ;
;![]() 时,
时,![]() ..........4分
..........4分
所以当![]() 时,
时,![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() ,
,
当![]() 时,
时,![]() 的减区间是
的减区间是![]() ,增区间是
,增区间是![]() .............. 6分
.............. 6分
(2)![]() 时,
时,![]() ,由
,由![]() 得:
得:![]() ,
,
设![]() ,
,
![]() ,.......................8分
,.......................8分
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,..........................10分
上递减,..........................10分
![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .............12分
.............12分


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】国家实行二孩生育政策后,为研究家庭经济状况对生二胎的影响,某机构在本地区符合二孩生育政策的家庭中,随机抽样进行了调查,得到如下的列联表:
经济状况好 | 经济状况一般 | 合计 | |
愿意生二胎 | 50 | ||
不愿意生二胎 | 20 | 110 | |
合计 | 210 |
(1)请完成上面的列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为家庭经济状况与生育二胎有关?
的前提下认为家庭经济状况与生育二胎有关?
(2)若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭,则经济状况好和经济状况一般的家庭分别应抽取多少个?
(3)在(2)的条件下,从中随机抽取2个家庭,求2个家庭都是经济状况好的概率.
附:![]()
|
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集成电路E由3个不同的电子元件组成,现由于元件老化,3个电子元件能正常工作的概率分别降为![]() ,
,![]() ,
,![]() ,且每个电子元件能否正常工作相互独立。若3个电子元件中至少有2个正常工作,则E能正常工作,否则就需要维修,且维修集成电路E所需要费用为100元。
,且每个电子元件能否正常工作相互独立。若3个电子元件中至少有2个正常工作,则E能正常工作,否则就需要维修,且维修集成电路E所需要费用为100元。
(Ⅰ)求集成电路E需要维修的概率;
(Ⅱ)若某电子设备共由2个集成电路E组成,设X为该电子设备需要维修集成电路所需费用。求X的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年巴西奥运会的周边商品有80%左右为“中国制造”,所有的厂家都是经过层层筛选才能获此殊荣.甲、乙两厂生产同一产品,为了解甲、乙两厂的产品质量,以确定这一产品最终的供货商,采用分层抽样的方法从甲、乙两厂生产的产品共98件中分别抽取9件和5件,测量产品中的微量元素的含量(单位:毫克).下表是从乙厂抽取的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
| 169 | 178 | 166 | 175 | 180 |
| 75 | 80 | 77 | 70 | 81 |
(1)求乙厂生产的产品数量:
(2)当产品中的微量元素![]() 满足:
满足:![]() ,且
,且![]() 时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量:
时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量:
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图“月亮图”是由曲线![]() 与
与![]() 构成,曲线
构成,曲线![]() 是以原点
是以原点![]() 为中点,
为中点, ![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以
是以![]() 为顶点,
为顶点, ![]() 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, ![]() 是两条曲线的一个交点.
是两条曲线的一个交点.
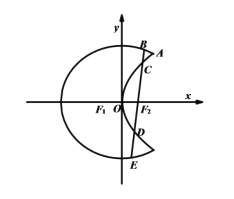
(Ⅰ)求曲线![]() 和
和![]() 的方程;
的方程;
(Ⅱ)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于
依次交于![]() 四点,若
四点,若![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,问:
的中点,问: ![]() 是否为定值?若是求出该定值;若不是说明理由.
是否为定值?若是求出该定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率![]() ,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,下图是根据刘徽的“割圆术”思想设计的一个程序框图,若运行该程序,则输出的
,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,下图是根据刘徽的“割圆术”思想设计的一个程序框图,若运行该程序,则输出的![]() 的值为( )(参考数据:
的值为( )(参考数据: ![]() ,
, ![]() ,
, ![]() )
)
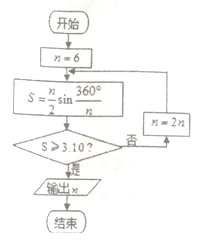
A. 24 B. 30 C. 36 D. 48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①命题“x0∈R,x+1>3x0”的否定是“x∈R,x2+1≤3x”;
②“函数f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
③x2+2x≥ax在x∈[1,2]上恒成立(x2+2x)min≥(ax)max在x∈[1,2]上恒成立;
④“平面向量a与b的夹角是钝角”的充要条件是“a·b<0”.
A.1 B.2
C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com