分析:(1)根据函数分段的表达式,分别将x=
-和x=
代入函数的第1表达式和第3表达式,即可得到f(
-)和f
()的值;
(2)根据函数的定义域和各范围内的表达式,结合一次函数、二次函数的图象作法,可得函数f(x)如图所示的简图;
(3)由(2)所作出的函数图象,结合一次函数和二次函数的性质,即可得到函数f(x)的最大、最小值,由此即可得到函数f(x)的值域.
解答:解:(1)∵-1≤
-<0,∴f(
-)=-(
-)=
∵1≤
≤2,∴f
()=
即f(
-)=
且f
()=
;
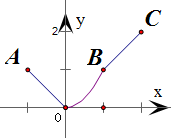
(2)当-1≤x<0时,f(x)=-x,可得图象是以A(-1,1)和原点为端点的线段;
当0≤x<1时,f(x)=x
2,可得图象是抛物线y=x
2位原点与B(1,1)之间的弧;
当1≤x≤2时,f(x)=x,可得图象是以B(1,1)和C(2,2)为端点的线段
因此,可作出函数y=f(x)的简图,如右图所示;
(3)根据一次函数和二次函数的单调性,结合作出(2)的图象,
可得函数f(x)的最小值为f(0)=0,最大值为f(2)=2
因此,函数f(x)的值域是[0,2]
点评:本题给出分段函数,求特殊的函数值并作函数的简图,着重考查了分段函数的含义,以及一次、二次函数的图象与性质和函数值域的求法等知识,属于基础题.



