
| A. | $-\frac{16}{23}$ | B. | $-\frac{23}{16}$ | C. | $\frac{16}{23}$ | D. | $\frac{23}{16}$ |
分析 由函数是奇函数得到f(-x)=-f(x)和f(x+2)=f(x)把则$f({log_{\frac{1}{2}}}23)$进行变形得到-f($lo{g}_{2}\frac{23}{16}$),由$lo{g}_{2}\frac{23}{16}$∈(0,1)满足f(x)=2x,求出即可.
解答 解:根据对数函数的图象可知 $f({log_{\frac{1}{2}}}23)$<0,且$f({log_{\frac{1}{2}}}23)$=-log223;
奇函数f(x)满足f(x+2)=f(x)和f(-x)=-f(x)
则$f({log_{\frac{1}{2}}}23)$=f(-log223)=-f(log223)=-f(log223-4)=-f($lo{g}_{2}\frac{23}{16}$),
因为$lo{g}_{2}\frac{23}{16}$∈(0,1)
∴-f($lo{g}_{2}\frac{23}{16}$)=$-{2}^{lo{g}_{2}\frac{23}{16}}$=$-\frac{23}{16}$,
故选:B
点评 考查学生应用函数奇偶性的能力,函数的周期性的掌握能力,以及运用对数的运算性质能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:
从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
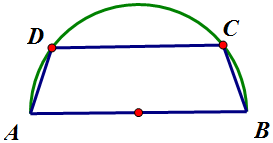 有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.
有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈[0,2π],sinx≥1 | B. | ¬p:?x∈[-2π,0],sinx>1 | ||
| C. | ¬p:?x∈[0,2π],sinx>1 | D. | ¬p:?x∈[-2π,0],sinx>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com