
【题目】在一项研究中,为尽快攻克某一课题,某生物研究所分别设立了甲、乙两个研究小组同时进行对比试验,现随机在这两个小组各抽取40个数据作为样本,并规定试验数据落在[495,510)之内的数据作为理想数据,否则为不理想数据.试验情况如表所示

(1)由以上统计数据完成下面2×2列联表;
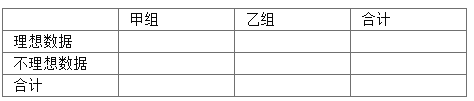
(2)判断是否有90%的把握认为抽取的数据为理想数据与对两个研究小组的选择有关;说明你的理由;(下面的临界值表供参考)

(参考公式: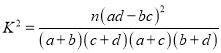 其中n=a+b+c+d)
其中n=a+b+c+d)
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人去某地务工,其工作受天气影响,雨天不能出工,晴天才能出工.其计酬方式有两种,方式一:雨天没收入,晴天出工每天![]() 元;方式而:雨天每天
元;方式而:雨天每天![]() 元,晴天出工每天
元,晴天出工每天![]() 元;三人要选择其中一种计酬方式,并打算在下个月(
元;三人要选择其中一种计酬方式,并打算在下个月(![]() 天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(
天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(![]() 天)为依据作出选择;乙和丙在分析了当地近
天)为依据作出选择;乙和丙在分析了当地近![]() 年此月的下雨天数(
年此月的下雨天数(![]() )的频数分布表(见下表)后,乙以频率最大的
)的频数分布表(见下表)后,乙以频率最大的![]() 值为依据作出选择,丙以
值为依据作出选择,丙以![]() 的平均值为依据作出选择.
的平均值为依据作出选择.
| 8 | 9 | 10 | 11 | 12 | 13 |
频数 | 3 | 1 | 2 | 0 | 2 | 1 |
(Ⅰ)试判断甲、乙、丙选择的计酬方式,并说明理由;
(Ⅱ)根据统计范围的大小,你觉得三人中谁的依据更有指导意义?
(Ⅲ)以频率作为概率,求未来三年中恰有两年,此月下雨不超过![]() 天的概率.
天的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形理论是当今世界十分风靡和活跃的新理论、新学科。其中,把部分与整体以某种方式相似的形体称为分形。分形是一种具有自相似特性的现象,图象或者物理过程。标准的自相似分形是数学上的抽象,迭代生成无限精细的结构。也就是说,在分形中,每一组成部分都在特征上和整体相似,只仅仅是变小了一些而已,谢尔宾斯基三角形就是一种典型的分形,是由波兰数学家谢尔宾斯基在1915年提出的,按照如下规律依次在一个黑色三角形内去掉小三角形则当![]() 时,该黑色三角形内共去掉( )个小三角形
时,该黑色三角形内共去掉( )个小三角形

A. 81 B. 121 C. 364 D. 1093
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已经成为当下热门的健身方式,韩梅梅的微信朋友圈内有800为好友参与了“微信运动”.他随机抽取了50为微信好友(男、女各25人),统计其在某一天的走路步数.其中女性好友的走路步数数据记录如下:
12860 8320 10231 6734 7323 8430 3200 4543 11123 9860
8753 6454 7292 4850 10222 9734 7944 9117 6421 2980
1123 1786 2436 3876 4326
男性好友走路步数情况可以分为五个类别![]() (0-2000步)(说明:“0-2000”表示大于等于0,小于等于2000,下同),
(0-2000步)(说明:“0-2000”表示大于等于0,小于等于2000,下同),![]() (2001-5000)、
(2001-5000)、![]() (5001-8000)、
(5001-8000)、![]() (8001-10000步)、
(8001-10000步)、![]() (10001步及以上),且
(10001步及以上),且![]() 三中类型的人数比例为
三中类型的人数比例为![]() ,将统计结果绘制如图所示的柱形图.
,将统计结果绘制如图所示的柱形图.
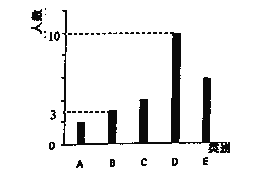
若某人一天的走路步数超过8000步则被系统评定为“积极型”,否则被系统评定为“懈怠型”.
(1)若以韩梅梅抽取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计韩梅梅的微信好友圈里参与“微信运动”的800名好友中,每天走路步数在5001-10000步的人数;
(2)请根据选取的样本数据完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | 25 | ||
女 | 25 | ||
总计 | 30 |
(3)若从韩梅梅当天选取的步数大于10000的好友中按男女比例分层选取5人进行身体状况调查,然后再从这5位好友中选取2人进行访谈,求至少有一位女性好友访谈的概率.
参考公式: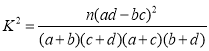 ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
【答案】(1)见解析;(2)![]()
【解析】(1)证明略;(2)直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() .或直线
.或直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]()
试题分析:(1)设出点的坐标,联立直线与抛物线的方程,由斜率之积为![]() 可得
可得![]() ,即得结论;(2)结合(1)的结论求得实数
,即得结论;(2)结合(1)的结论求得实数![]() 的值,分类讨论即可求得直线
的值,分类讨论即可求得直线![]() 的方程和圆
的方程和圆![]() 的方程.
的方程.
试题解析:(1)设![]() ,
,![]() .
.
由![]() 可得
可得![]() ,则
,则![]() .
.
又![]() ,故
,故![]() .
.
因此![]() 的斜率与
的斜率与![]() 的斜率之积为
的斜率之积为![]() ,所以
,所以![]() .
.
故坐标原点![]() 在圆
在圆![]() 上.
上.
(2)由(1)可得![]() .
.
故圆心![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 的半径
的半径![]() .
.
由于圆![]() 过点
过点![]() ,因此
,因此![]() ,故
,故![]() ,
,
即![]() ,
,
由(1)可得![]() .
.
所以![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆心
,圆心![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 的半径为
的半径为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆心
,圆心![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 的半径为
的半径为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.
【名师点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系;在解决直线与抛物线的位置关系时,要特别注意直线与抛物线的对称轴平行的特殊情况.中点弦问题,可以利用“点差法”,但不要忘记验证![]() 或说明中点在曲线内部.
或说明中点在曲线内部.
【题型】解答题
【结束】
21
【题目】已知函数![]() .
.
(1)若![]() ,求a的值;
,求a的值;
(2)设m为整数,且对于任意正整数n,![]() ,求m的最小值.
,求m的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com