练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在四面体中， ，二面角的余弦值是，则该四面体外接球的表面积是（ ）

    A. B. C. D.

    【答案】B

    【解析】因为所以，设的中点为，连接，则三角形的外心为在线段上，且，又三角形的外心为，又，所以平面，过垂直于平面的直线与过垂直于平面的直线交于点，则为四面体外接球的球

    心，又，所以，

    所以，设外接圆半径为，则，所以，故选B.

    点睛:空间几何体与球接、切问题的求解方法

    (1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．

    (2)若球面上四点构成的三条线段两两互相垂直，且，一般把有关元素“补形”成为一个球内接长方体，利用求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某市的天气预报中,有“降水概率预报”,例如预报“明天降水概率为90%”,这是指(　　)

    A. 明天该地区约有90%的地方会降水,其余地方不降水

    B. 明天该地区约90%的时间会降水,其余时间不降水

    C. 气象台的专家中,有90%认为明天会降水,其余的专家认为不降水

    D. 明天该地区降水的可能性为90%

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x），g（x）分别由下表给出．

    x

    1

    2

    3

    f（x）

    2

    3

    1

    x

    1

    2

    3

    g（x）

    3

    2

    1

    则f[g（1）]的值为；当g[f（x）]＝2时，x＝ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，是的中点，.

    （1）已知，，求证：平面；

    （2）已知分别是和的中点，求证： 平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线，半径为2的圆与相切，圆心在轴上且在直线的右上方.

    （1）求圆的方程；

    （2）若直线过点且与圆交于两点（在轴上方，在轴下方），问在轴正半轴上是否存在定点，使得轴平分？若存在，请求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={2,9},B={m2,2}，若A=B,则实数m的值为 （ ）
    A.3
    B.－3
    C.9
    D.±3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个年级有16个班级，每个班级学生从1到50号编排，为了交流学习经验，要求每班编号为14的同学留下进行交流，这里运用的是 （ ）

    A. 分层抽样 B. 抽签法 C. 系统抽样 D. 随机数表法

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知极坐标系的极点在直角坐标系的原点处，极轴与轴非负半轴重合，直线的参数方程为: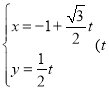为参数）,曲线的极坐标方程为:.

    （1）写出曲线的直角坐标方程和直线的普通方程;

    （2）设直线与曲线相交于两点,求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

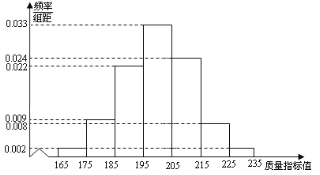
    【题目】从某企业的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：

    （Ⅰ）求这500件产品质量指标值的样本平均数和样本方差（用同一组数据用该区间的中点值用代表）；

    （Ⅱ）由频率分布直方图可以认为，这种产品的质量指标值服从正态分布，其中近似为样本平均数，近似为样本方差.

    （i）利用该正态分布，求；

    （ii）某用户从该企业购买了100件这种产品，记表示这100件产品中质量指标值位于区间的产品件数，利用（i）的结果，求.

    附：，若，则，

    查看答案和解析>>

    同步练习册答案