
| A. | (-$\frac{π}{8}$,0) | B. | (-$\frac{π}{4}$,0) | C. | ($\frac{π}{8}$,0) | D. | ($\frac{π}{4}$,0) |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 1 | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
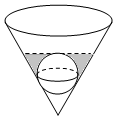 祖暅,字景烁,祖冲之之子,南北朝时代的伟大科学家.祖暅在数学上有突出的贡献,他在实践的基础上,于5世纪末提出下面的计算原理:祖暅原理:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,请同学们用祖暅原理解决如下问题:如图,有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,再注入水,使水面与球正好相切(而且球与倒圆锥相切效果很好,水不能流到倒圆锥容器底部),然后将球取出,则这时容器中水的深度为$\root{3}{15}$r.
祖暅,字景烁,祖冲之之子,南北朝时代的伟大科学家.祖暅在数学上有突出的贡献,他在实践的基础上,于5世纪末提出下面的计算原理:祖暅原理:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等,请同学们用祖暅原理解决如下问题:如图,有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,再注入水,使水面与球正好相切(而且球与倒圆锥相切效果很好,水不能流到倒圆锥容器底部),然后将球取出,则这时容器中水的深度为$\root{3}{15}$r.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 3 | C. | 27或3 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com