已知命题p:|x-1|+|x+1|≥3a恒成立,命题q:y=(2a-1)x为减函数,若p且q为真命题,则a的取值范围是________.
(
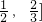
分析:利用绝对值的几何意义结合恒成立的解决方法可求的命题p为真时a的范围,然后用指数函数的知识可以求出命题q为真时a的范围,进而求交集得出a的取值范围.
解答:∵p且q为真命题,
∴命题p与命题q均为真命题.
当命题p为真命题时:
∵|x-1|+|x+1|≥3a恒成立,
∴只须|x-1|+|x+1|的最小值≥3a即可,
而有绝对值的几何意义得|x-1|+|x+1|≥2,
即|x-1|+|x+1|的最小值为2,
∴应有:3a≤2,解得:a≤

,①.
当命题q为真命题时:
∵y=(2a-1)
x为减函数,
∴应有:0<2a-1<1,解得:

,②.
综上①②得,a的取值范围为:
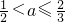
即:(

].
故答案为:(

].
点评:本题以恒成立为载体结合绝对值的几何意义、指数函数的单调性考查复合命题的真假判断,属于综合性的题目,要加以训练.

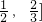
 ,①.
,①. ,②.
,②.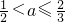 即:(
即:( ].
]. ].
].
