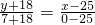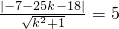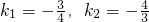Question

一束光线通过点M（25，18）射到x轴上，入射点为A，经反射后射到圆C：x²+（y-7）²=25上．
（Ⅰ）求经过圆心的反射光线所在直线的方程；　
（Ⅱ）求点A在x轴上的活动范围．

Answer 1

解：（Ⅰ）点M（25，18）射到x轴上，关于x轴的对称点M′（25，-18）
所以反射光线过M′（25，-18），圆心（0，7）
所以直线为
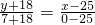
即y=-x+7；
（Ⅱ）A的取值范围是反射后射到圆C：x²+（y-7）²=25上，临界状态时的取值范围．
因为x轴的对称点M′（25，-18）
所以设直线y=k（x-25）-18，即kx-y-25k-18=0
利用圆心到直线的距离等于半径可得：
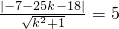
∴12k²+25k+12=0
∴
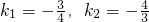
所以对应的方程分别为：3x+4y-3=0，4x+3y-46=0
此时令A（x，0）
所以x分别为1，11.5
所以A的活动范围[1，11.5]．
分析：（Ⅰ）求出点M（25，18）关于x轴的对称点M′，利用反射光线过M′与圆心，即可求得直线方程；
（Ⅱ）A的取值范围是反射后射到圆C：x²+（y-7）²=25上，临界状态时的取值范围．利用圆心到直线的距离等于半径，从而可求得临界状态时反射光线的方程，进而可求A的活动范围．
点评：本题以圆的标准方程为载体，考查直线方程，考查对称性，解题的关键是A的取值范围是反射后射到圆C：x²+（y-7）²=25上，临界状态时的取值范围