
【题目】某中学为弘扬优良传统,展示80年来的办学成果,特举办“建校80周年教育成果展示月”活动。现在需要招募活动开幕式的志愿者,在众多候选人中选取100名志愿者,为了在志愿者中选拔出节目主持人,现按身高分组,得到的频率分布表如图所示.


(1)请补充频率分布表中空白位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为选拔出主持人,决定在第3、4、5组中用分层抽样抽取6人上台,求第3、4、5组每组各抽取多少人?
(3)在(2)的前提下,主持人会在上台的6人中随机抽取2人表演诗歌朗诵,求第3组至少有一人被抽取的概率?
参考公式:
 .
.
【答案】(1)见解析; (2)3,2,1; (3)![]() .
.
【解析】
(1)根据频率、频数与样本容量的关系,求出对应的数值,画出频率分布直方图;
(2)利用分层抽样原理,求出各小组应抽取的人数;
(3)利用列举法求出基本事件数,计算对应的概率值.
(1)第二组的频数为![]() ,故第三组的频数为
,故第三组的频数为![]() ,故第三组的频率为0.3,第五组的频率为0.1,补全后频率分布表为:
,故第三组的频率为0.3,第五组的频率为0.1,补全后频率分布表为:
组号 | 分组 | 频数 | 频率 |
第一组 |
|
| 0.05 |
第二组 |
|
| 0.35 |
第三组 |
|
| 0.3 |
第四组 |
|
| 0.2 |
第五组 |
|
| 0.1 |
合计 | 100 | 1 |
频率分布直方图为:
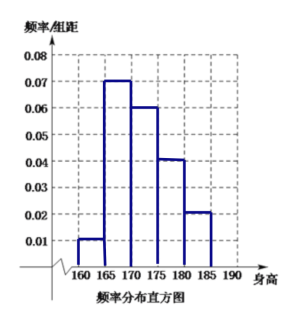
(2)第三组、第四组、第五组的频率之比3:2:1,
故第三组、第四组、第五组抽取的人数分别为3,2,1.
(3)设第三组中抽取的三人为![]() ,第四组中抽取的两人为
,第四组中抽取的两人为![]() ,第五组中抽取的一人为C,则6人中任意抽取两人,所有的基本事件如下:
,第五组中抽取的一人为C,则6人中任意抽取两人,所有的基本事件如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故第三组中至少有1人被抽取的概率为![]() .
.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线方程为![]() .
.
(1)求以定点![]() 为中点的弦所在的直线方程;
为中点的弦所在的直线方程;
(2)以定点![]() 为中点的弦存在吗?若存在,求出其所在的直线方程;若不存在,请说明理由.
为中点的弦存在吗?若存在,求出其所在的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 、
、![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 和曲线
和曲线![]() 只有一个交点,求
只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,且过点
,且过点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 为抛物线
为抛物线![]() 与椭圆
与椭圆![]() 的一个公共点,且
的一个公共点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆内一点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,设直线
两点,设直线![]() ,
,![]() (
(![]() 为坐标原点)的斜率分别为
为坐标原点)的斜率分别为![]() ,
,![]() ,若对任意
,若对任意![]() ,存在实数
,存在实数![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.

(1)求直线![]() 所过定点A的坐标;
所过定点A的坐标;
(2)求直线![]() 被圆C所截得的弦长最短时直线
被圆C所截得的弦长最短时直线![]() 的方程及最短弦长;
的方程及最短弦长;
(3)已知点M(-3,4),在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有![]() 为一常数, 试求所有满足条件的点N的坐标及该常数.
为一常数, 试求所有满足条件的点N的坐标及该常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=![]() .
.

(1)求证:AO⊥平面BCD;
(2)求二面角O﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为2。
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为2。
(1)求椭圆C的方程;
(2)椭圆C上是否存在一点P,使得当l绕F转到某一位置时,有![]() 成立?若存在,求点P的坐标与直线l的方程;若不存在,说明理由。
成立?若存在,求点P的坐标与直线l的方程;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com