
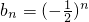 ,n∈N*,判断{an}、{bn}是否为“p-摆动数列”,并说明理由;
,n∈N*,判断{an}、{bn}是否为“p-摆动数列”,并说明理由;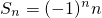 ,试问:数列{dn}是否为“p-摆动数列”,若是,求出p的取值范围;若不是,说明理由.
,试问:数列{dn}是否为“p-摆动数列”,若是,求出p的取值范围;若不是,说明理由.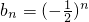 ,于是
,于是 对任意n成立,
对任意n成立, ,
, ,
, 成立,
成立,

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
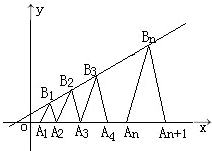 函数y=f(x)是定义在R上的偶函数,且f(-1+x)=f(-1-x),当x∈[-2,-1]时,f(x)=t(x+2)3-t(x+2)(t∈R),记函数y=f(x)的图象在(
函数y=f(x)是定义在R上的偶函数,且f(-1+x)=f(-1-x),当x∈[-2,-1]时,f(x)=t(x+2)3-t(x+2)(t∈R),记函数y=f(x)的图象在(| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 对任意函数f(x),x∈D,可按如图构造一个数列发生器,记由数列发生器产生数列{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,记由数列发生器产生数列{xn}.| 4x-2 |
| x+1 |
| 49 |
| 65 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
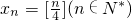 ,则x1+x2+…+x4n=________.
,则x1+x2+…+x4n=________.查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京市朝阳区高一(下)期末数学试卷(解析版) 题型:填空题
 ,则x1+x2+…+x4n= .
,则x1+x2+…+x4n= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com