
【题目】已知 ![]() .
.
(1)若函数![]() 的值域为
的值域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)函数![]() 的值域为
的值域为![]() ,即是不等式
,即是不等式![]() 的解集为
的解集为![]() ,利用二次函数性质可得判别式小于零即可得结果;(2)根据区间
,利用二次函数性质可得判别式小于零即可得结果;(2)根据区间![]() 即是函数
即是函数![]() 定义域的子集又是二次函数减区间的子集,列不等式组求解即可.
定义域的子集又是二次函数减区间的子集,列不等式组求解即可.
试题解析:(1)f(x)值域为R,令g(x)=x2﹣mx﹣m, 则g(x)取遍所有的正数
即△=m2+4m≥0
∴m≥0或m≤﹣4;
(2)由题意知 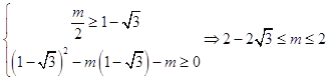 .
.
【方法点晴】本题主要考查函数的定义域、值域及利用单调性求参数的范围,属于中档题. 利用单调性求参数的范围的常见方法:① 视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数需注意若函数在区间![]() 上是单调的,则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式
上是单调的,则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式![]() 或
或![]() 恒成立问题求参数范围,本题(2)是利用方法 ① 求解的.
恒成立问题求参数范围,本题(2)是利用方法 ① 求解的.


科目:高中数学 来源: 题型:
【题目】某市某水产养殖户进行小龙虾销售,已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系为:
(天)之间的函数关系为:
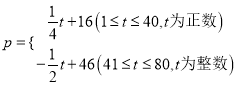 ,日销售量
,日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
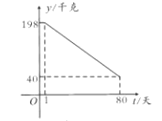
(1)求日销售量![]() 与时间
与时间![]() 的函数关系式?
的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠![]() 元给村里的特困户,在这前40天中,每天扣除捐赠后的日销售利润随时间
元给村里的特困户,在这前40天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为![]() 的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
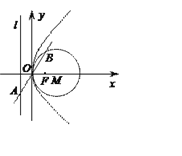
(1)求⊙M和抛物线C的方程;
(2)若P为抛物线C上的动点,求![]() 的最小值;
的最小值;
(3)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值为2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值为2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg(ax﹣bx),且f(1)=lg2,f(2)=lg12
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)m为何值时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com