
°æƒø°ø»Àø⁄∆Ωæ˘‘§∆⁄ Ÿ√¸ «◊€∫œ∑¥”≥»À√«Ω°øµÀÆ∆Ωµƒª˘±æ÷∏±Í.![]() ƒÍµ⁄¡˘¥Œ»´π˙»Àø⁄∆’≤È◊ ¡œ±Ì√˜£¨ÀÊ◊≈Œ“π˙…Áª·æ≠º√µƒøÏÀŸ∑¢’𣨻À√Ò…˙ªÓÀÆ∆Ωµƒ≤ª∂œÃ·∏þ“‘º∞“Ω¡∆Œ¿…˙±£’œÃÂœµµƒ÷≤ΩÕÍ…∆£¨Œ“π˙»Àø⁄∆Ωæ˘‘§∆⁄ Ÿ√¸ºÃ–¯—”≥§£¨π˙√Ò’˚ÃÂΩ°øµÀÆ∆Ω”–Ωœ¥Û∑˘∂»µƒÃ·∏þ.œ¬ÕºÃÂœ÷¡ÀŒ“π˙∆Ωæ˘‘§∆⁄ Ÿ√¸±‰ªØ«Èøˆ£¨“¿æð¥ÀÕº£¨œ¬¡–Ω·¬€¥ÌŒÛµƒ «£® £©
ƒÍµ⁄¡˘¥Œ»´π˙»Àø⁄∆’≤È◊ ¡œ±Ì√˜£¨ÀÊ◊≈Œ“π˙…Áª·æ≠º√µƒøÏÀŸ∑¢’𣨻À√Ò…˙ªÓÀÆ∆Ωµƒ≤ª∂œÃ·∏þ“‘º∞“Ω¡∆Œ¿…˙±£’œÃÂœµµƒ÷≤ΩÕÍ…∆£¨Œ“π˙»Àø⁄∆Ωæ˘‘§∆⁄ Ÿ√¸ºÃ–¯—”≥§£¨π˙√Ò’˚ÃÂΩ°øµÀÆ∆Ω”–Ωœ¥Û∑˘∂»µƒÃ·∏þ.œ¬ÕºÃÂœ÷¡ÀŒ“π˙∆Ωæ˘‘§∆⁄ Ÿ√¸±‰ªØ«Èøˆ£¨“¿æð¥ÀÕº£¨œ¬¡–Ω·¬€¥ÌŒÛµƒ «£® £©
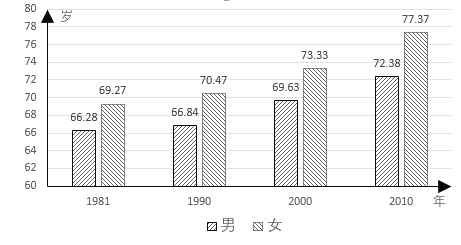
A.ƒ––‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸÷Ω•—”≥§
B.≈Æ–‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸÷Ω•—”≥§
C.ƒ––‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸—”≥§∑˘∂»¬‘∏þ”⁄≈Æ–‘
D.≈Æ–‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸—”≥§∑˘∂»¬‘∏þ”⁄ƒ––‘
°æ¥∞∏°øC
°æΩ‚Œˆ°ø
¥”Õº–Œ÷–µƒ ˝æ𱉪Øø…≈–∂œA°¢B—°œÓµƒ’˝ŒÛ£ªº∆À„≥ˆƒ––‘∫Õ≈Æ–‘∆Ωæ˘‘§∆⁄ Ÿ√¸—”≥§∑˘∂»£¨ø…≈–∂œC°¢D—°œÓµƒ’˝ŒÛ£¨◊€∫œø…µ√≥ˆΩ·¬€.
”…Õº–Œø…÷™£¨ƒ––‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸÷Ω•—”≥§£¨≈Æ–‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸“≤‘⁄÷Ω•—”≥§£¨A°¢B—°œÓæ˘’˝»∑£ª
¥”![]() ƒÍµΩ
ƒÍµΩ![]() ƒÍ£¨ƒ––‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸µƒ‘ˆ∑˘Œ™
ƒÍ£¨ƒ––‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸µƒ‘ˆ∑˘Œ™![]() £¨≈Æ–‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸µƒ‘ˆ∑˘Œ™
£¨≈Æ–‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸µƒ‘ˆ∑˘Œ™![]() £¨
£¨
À˘“‘£¨≈Æ–‘µƒ∆Ωæ˘‘§∆⁄ Ÿ√¸—”≥§∑˘∂»¬‘∏þ”⁄ƒ––‘£¨C—°œÓ¥ÌŒÛ£¨D—°œÓ’˝»∑.
π —°£∫C.


 ÷∑÷∞Ÿ∑÷∞ŸºÏ≤‚æ̵•‘™∆⁄ƒ©≤‚ ‘æÌœµ¡–¥∞∏
÷∑÷∞Ÿ∑÷∞ŸºÏ≤‚æ̵•‘™∆⁄ƒ©≤‚ ‘æÌœµ¡–¥∞∏ –°—ß∆⁄ƒ©±Í◊º ‘æÌœµ¡–¥∞∏
–°—ß∆⁄ƒ©±Í◊º ‘æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™÷±œþ![]() µƒ≤Œ ˝∑Ω≥ÃŒ™
µƒ≤Œ ˝∑Ω≥ÃŒ™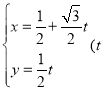 Œ™≤Œ ˝£©£¨“‘◊¯±Í‘≠µ„Œ™º´µ„£¨
Œ™≤Œ ˝£©£¨“‘◊¯±Í‘≠µ„Œ™º´µ„£¨![]() ÷·µƒ’˝∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£¨«˙œþ
÷·µƒ’˝∞Î÷·Œ™º´÷·Ω®¡¢º´◊¯±Íœµ£¨«˙œþ![]() µƒº´◊¯±Í∑Ω≥ÃŒ™
µƒº´◊¯±Í∑Ω≥ÃŒ™![]() .
.
£®1£©«Û÷±œþ![]() µƒ∆’Õ®∑Ω≥Ã∫Õ«˙œþ
µƒ∆’Õ®∑Ω≥Ã∫Õ«˙œþ![]() µƒ÷±Ω«◊¯±Í∑Ω≥ãª
µƒ÷±Ω«◊¯±Í∑Ω≥ãª
£®2£©…˵„![]() £¨÷±œþ
£¨÷±œþ![]() ”Ϋ˙œþ
”Ϋ˙œþ![]() Ωª”⁄
Ωª”⁄![]() ¡Ωµ„£¨«Û
¡Ωµ„£¨«Û![]() µƒ÷µ.
µƒ÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() π˝µ„
π˝µ„![]() £¨«“À¸µƒ“ª∏ˆΩ𵄔Î≈◊ŒÔœþ
£¨«“À¸µƒ“ª∏ˆΩ𵄔Î≈◊ŒÔœþ![]() µƒΩπµ„œýÕ¨£Æ÷±œþ
µƒΩπµ„œýÕ¨£Æ÷±œþ![]() π˝µ„
π˝µ„![]() £¨«“”ÎÕ÷‘≤
£¨«“”ÎÕ÷‘≤![]() œýΩª”⁄
œýΩª”⁄![]() ¡Ωµ„£Æ
¡Ωµ„£Æ
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©»Ù÷±œþ![]() µƒ“ª∏ˆ∑ΩœÚœÚ¡øŒ™
µƒ“ª∏ˆ∑ΩœÚœÚ¡øŒ™![]() £¨«Û
£¨«Û![]() µƒ√ʪ˝£®∆‰÷–
µƒ√ʪ˝£®∆‰÷–![]() Œ™◊¯±Í‘≠µ„£©£ª
Œ™◊¯±Í‘≠µ„£©£ª
£®3£© ‘Œ £∫‘⁄![]() ÷·…œ «∑ҥʑ⁄µ„
÷·…œ «∑ҥʑ⁄µ„![]() £¨ πµ√
£¨ πµ√![]() Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„
Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„![]() µƒ◊¯±Í∫Õ∂®÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í∫Õ∂®÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤C£∫![]() µƒ∂Ã÷·≥§Œ™2£¨¿Î–ƒ¬ Œ™
µƒ∂Ã÷·≥§Œ™2£¨¿Î–ƒ¬ Œ™![]() £¨◊Û∂•µ„Œ™A£¨π˝µ„Aµƒ÷±œþl”ÎCΩª”⁄¡Ì“ª∏ˆµ„M£¨«“”Î÷±œþx£ΩtΩª”⁄µ„N£Æ
£¨◊Û∂•µ„Œ™A£¨π˝µ„Aµƒ÷±œþl”ÎCΩª”⁄¡Ì“ª∏ˆµ„M£¨«“”Î÷±œþx£ΩtΩª”⁄µ„N£Æ
£®1£©«ÛÕ÷‘≤Cµƒ∑Ω≥ãª
£®2£© «∑ҥʑ⁄ µ ˝t£¨ πµ√![]() Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û µ ˝tµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
Œ™∂®÷µ£ø»Ù¥Ê‘⁄£¨«Û µ ˝tµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷±œþ![]() «π˝µ„
«π˝µ„![]() µƒ∂Ø÷±œþ£¨µ±
µƒ∂Ø÷±œþ£¨µ±![]() ”Α≤
”Α≤![]() œý«– ±£¨Õ¨ ±“≤∫Õ≈◊ŒÔœþ
œý«– ±£¨Õ¨ ±“≤∫Õ≈◊ŒÔœþ![]() œý«–.
œý«–.
£®1£©«Û≈◊ŒÔœþ![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©÷±œþ![]() ”Î≈◊ŒÔœþ
”Î≈◊ŒÔœþ![]() Ωª”⁄≤ªÕ¨µƒ¡Ωµ„
Ωª”⁄≤ªÕ¨µƒ¡Ωµ„![]() £¨”Α≤
£¨”Α≤![]() Ωª”⁄≤ªÕ¨µƒ¡Ωµ„A°¢B£¨
Ωª”⁄≤ªÕ¨µƒ¡Ωµ„A°¢B£¨![]() √ʪ˝Œ™
√ʪ˝Œ™![]() £¨
£¨![]() √ʪ˝Œ™
√ʪ˝Œ™![]() £¨µ±
£¨µ±![]() ±£¨«Û÷±œþ
±£¨«Û÷±œþ![]() µƒ∑Ω≥ãÆ
µƒ∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™µ„![]() ‘⁄Õ¨“ª∏ˆ«Úµƒ…œ,
‘⁄Õ¨“ª∏ˆ«Úµƒ…œ,![]() ,
,![]() ,
,![]() .»ÙÀƒ√ÊÃÂ
.»ÙÀƒ√ÊÃÂ![]() ê˝µƒ◊Ó¥Û÷µŒ™
ê˝µƒ◊Ó¥Û÷µŒ™![]() ,‘Ú’‚∏ˆ«Úµƒ±Ì√ʪ˝Œ™£® £©
,‘Ú’‚∏ˆ«Úµƒ±Ì√ʪ˝Œ™£® £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄µ•Œª‘≤O£∫x2+y2£Ω1…œ»Œ»°“ªµ„P£®x£¨y£©£¨‘≤O”Îx÷·’˝œÚµƒΩªµ„ «A£¨…ËΩ´OA»∆‘≠µ„O–˝◊™µΩOPÀ˘≥…µƒΩ«Œ™¶»£¨º«x£¨yπÿ”⁄¶»µƒ±Ì¥Ô Ω∑÷±Œ™x£Ωf£®¶»£©£¨y£Ωg£®¶»£©£¨‘Úœ¬¡–Àµ∑®’˝»∑µƒ «£®°°°°£©
A.x£Ωf£®¶»£© «≈º∫Ø ˝£¨y£Ωg£®¶»£© «∆Ê∫Ø ˝
B.x£Ωf£®¶»£©‘⁄![]() Œ™‘ˆ∫Ø ˝£¨y£Ωg£®¶»£©‘⁄
Œ™‘ˆ∫Ø ˝£¨y£Ωg£®¶»£©‘⁄![]() Œ™ºı∫Ø ˝
Œ™ºı∫Ø ˝
C.f£®¶»£©+g£®¶»£©°ð1∂‘”⁄![]() ∫„≥…¡¢
∫„≥…¡¢
D.∫Ø ˝t£Ω2f£®¶»£©+g£®2¶»£©µƒ◊Ó¥Û÷µŒ™![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–{an}µƒ∏˜œÓæ˘Œ™’˝ ˝£¨∆‰«∞nœÓ∫ÕSn¬˙◊„4Sn£Ωan2+2an£¨n° N*.…Ëbn£Ω£®©Å1£©nanan+1£¨TnŒ™ ˝¡–{bn}µƒ«∞nœÓ∫Õ£¨‘ÚT2n£Ω_____.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤C£∫![]() £®
£®![]() £©µƒΩπæýŒ™4£¨∆‰∂Ã÷·µƒ¡Ω∏ˆ∂Àµ„”Î≥§÷·µƒ“ª∏ˆ∂Àµ„ππ≥…’˝»˝Ω«–Œ.
£©µƒΩπæýŒ™4£¨∆‰∂Ã÷·µƒ¡Ω∏ˆ∂Àµ„”Î≥§÷·µƒ“ª∏ˆ∂Àµ„ππ≥…’˝»˝Ω«–Œ.
£®1£©«ÛÕ÷‘≤Cµƒ±Í◊º∑Ω≥ãª
£®2£©…ËFŒ™Õ÷‘≤Cµƒ◊ÛΩ𵄣¨TŒ™÷±œþ![]() …œ»Œ“‚“ªµ„£¨π˝F◊˜TFµƒ¥πœþΩªÕ÷‘≤C”⁄µ„P£¨Q.
…œ»Œ“‚“ªµ„£¨π˝F◊˜TFµƒ¥πœþΩªÕ÷‘≤C”⁄µ„P£¨Q.
£®i£©÷§√˜£∫OT∆Ω∑÷œþ∂ŒPQ£®∆‰÷–OŒ™◊¯±Í‘≠µ„£©£ª
£®ii£©µ±![]() ◊Ó–° ±£¨«Ûµ„Tµƒ◊¯±Í.
◊Ó–° ±£¨«Ûµ„Tµƒ◊¯±Í.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com