
【解析】若![]() ,必有
,必有![]() .构造函数:
.构造函数:![]() ,则
,则![]() 恒成立,故有函数
恒成立,故有函数![]() 在x>0上单调递增,即a>b成立.其余选项用同样方法排除.
在x>0上单调递增,即a>b成立.其余选项用同样方法排除.
【答案】A
科目:高中数学 来源:2013届福建省泉州市高二下学期期中文科数学试卷(解析版) 题型:解答题
(1)若 ,
, ,求证:
,求证: ;
;
(2)已知 ,且
,且 , 求证:
, 求证: 与
与 中至少有一个小于2.
中至少有一个小于2.
【解析】第一问利用均值不等式,可知

第二问中,

证明:(1)

(2)

查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市闸北区高考二模测试文科数学试卷(解析版) 题型:解答题
如图, ,
,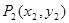 ,…,
,…, ,…是曲线
,…是曲线 上的点,
上的点, ,
, ,…,
,…, ,…是
,…是 轴正半轴上的点,且
轴正半轴上的点,且 ,
, ,…,
,…, ,…
均为斜边在
,…
均为斜边在 轴上的等腰直角三角形(
轴上的等腰直角三角形( 为坐标原点).
为坐标原点).
(1)写出 、
、 和
和 之间的等量关系,以及
之间的等量关系,以及 、
、 和
和 之间的等量关系;
之间的等量关系;
(2)求证: (
( );
);
(3)设 ,对所有
,对所有 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.

【解析】第一问利用有 ,
, 得到
得到
第二问证明:①当 时,可求得
时,可求得 ,命题成立;②假设当
,命题成立;②假设当 时,命题成立,即有
时,命题成立,即有 则当
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得
第三问

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即

解:(1)依题意,有 ,
, ,………………4分
,………………4分
(2)证明:①当 时,可求得
时,可求得 ,命题成立;
……………2分
,命题成立;
……………2分
②假设当 时,命题成立,即有
时,命题成立,即有 ,……………………1分
,……………………1分
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得 .
.
即
解得 (
( 不合题意,舍去)
不合题意,舍去)
即当 时,命题成立. …………………………………………4分
时,命题成立. …………………………………………4分
综上所述,对所有 ,
, . ……………………………1分
. ……………………………1分
(3)

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即
 .……………2分
.……………2分
由题意,有
 .
所以,
.
所以,
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(大纲卷解析版) 题型:选择题
已知函数y=x²-3x+c的图像与x恰有两个公共点,则c=
(A)-2或2 (B)-9或3 (C)-1或1 (D)-3或1
【解析】若函数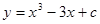 的图象与
的图象与 轴恰有两个公共点,则说明函数的两个极值中有一个为0,函数的导数为
轴恰有两个公共点,则说明函数的两个极值中有一个为0,函数的导数为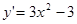 ,令
,令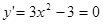 ,解得
,解得 ,可知当极大值为
,可知当极大值为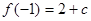 ,极小值为
,极小值为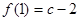 .由
.由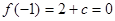 ,解得
,解得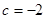 ,由
,由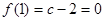 ,解得
,解得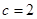 ,所以
,所以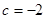 或
或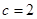 ,选A.
,选A.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com