练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】△ABC的内角A，B，C所对的边分别为a，b，c．向量 =（a， b）与 =（cosA，sinB）平行． （Ⅰ）求A；
    （Ⅱ）若a= ，b=2，求△ABC的面积．

    【答案】解：（Ⅰ）因为向量 =（a， b）与 =（cosA，sinB）平行， 所以asinB﹣ =0，由正弦定理可知：sinAsinB﹣ sinBcosA=0，因为sinB≠0，
    所以tanA= ，可得A= ；
    （Ⅱ）a= ，b=2，由余弦定理可得：a2=b2+c2﹣2bccosA，可得7=4+c2﹣2c，解得c=3，
    △ABC的面积为： =
    【解析】（Ⅰ）利用向量的平行，列出方程，通过正弦定理求解A；（Ⅱ）利用A，以及a= ，b=2，通过余弦定理求出c，然后求解△ABC的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣a，g（x）=a|x|，a∈R．
    （1）设F（x）=f（x）﹣g（x）． ①若a= ，求函数y=F（x）的零点；
    ②若函数y=F（x）存在零点，求a的取值范围．
    （2）设h（x）=f（x）+g（x），x∈[﹣2，2]，若对任意x1 ， x2∈[﹣2，2]，|h（x1）﹣h（x2）|≤6恒成立，试求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，几何体ABCDE中，△ABC是正三角形，EA和DC都垂直于平面ABC，且EA=AB=2a，DC=a，F、G分别为EB和AB的中点．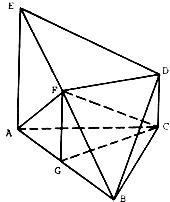

    （1）求证：FD∥平面ABC；
    （2）求二面角B﹣FC﹣G的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 的定义域为M．
    （1）求M；
    （2）当x∈M时，求 +1的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在公差不为零的等差数列{an}和等比数列{bn}中．已知a1=b1=1．a2=b2 ． a6=b3
    （1）求等差数列{an}的通项公式an和等比数列{bn}的通项公式bn；
    （2）求数列{anbn}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知α∈[ ， ]，β∈[﹣ ，0]，且（α﹣ ）3﹣sinα﹣2=0，8β3+2cos2β+1=0，则sin（ +β）的值为（ ）
    A.0
    B.
    C.
    D.1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体ABCD﹣A1B1C1D1中，E、F分别为CD、DD1的中点，则异面直线EF与A1C1所成角的余弦值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C过点A（1，4），B（3，2），且圆心在x轴上，求圆C的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一名心率过速患者服用某种药物后心率立刻明显减慢，之后随着药力的减退，心率再次慢慢升高，则自服药那一刻起，心率关于时间的一个可能的图象是（ ）
    A.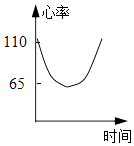
    B.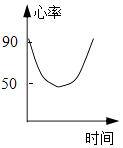
    C.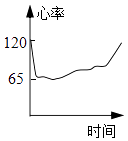
    D.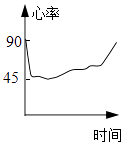

    查看答案和解析>>

    同步练习册答案