
(2)试用上面结论证明下面的命题:
若a,b,c∈R且|a|<1,|b|<1,|c|<1,则ab+bc+ca>-1.
| 证明:
(1)当k>0时,函数f(x)=kx+h在x∈R上是增函数,m<x<n,f(x)>f(m)>0; 当k<0时,函数f(x)=kx+h在x∈R上是减函数,m<x<n,f(x)>f(n)>0. 所以对于任意x∈(m,n)都有f(x)>0成立. (2)将ab+bc+ca+1写成(b+c)a+bc+1,构造函数f(x)=(b+c)x+bc+1.则 f(a)=(b+c)a+bc+1. 当b+c=0时,即b=-c, f(a)=bc+1=-c2+1. 因为|c|<1,所以f(a)=-c2+1>0. 当b+c≠0时,f(x)=(b+c)x+bc+1为x的一次函数. 因为|b|<1,|c|<1, f(1)=b+c+bc+1=(1+b)(1+c)>0, f(-1)=-b-c+bc+1=(1-b)(1-c)>0. 由问题(1)对于|a|<1的一切值f(a)>0,即 (b+c)a+bc+1=ab+ac+bc+1>0.
|


科目:高中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x2 |
| x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
(1)一次函数f(x)=kx+h(k≠0),若m<n有f(m)>0,f(n)>0,则对于任意x∈(m,n)都有f(x)>0,试证明之;
(2)试用上面结论证明下面的命题:
若a,b,c∈R且|a|<1,|b|<1,|c|<1,则ab+bc+ca>-1.
查看答案和解析>>
科目:高中数学 来源:南通高考密卷·数学(理) 题型:044
已知集合M是满足下列性质的函数f(x)的全体:存在非零常数k,对任意x∈D(D为函数的定义域),等式f(kx)=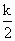 +f(x)成立.
+f(x)成立.
(1)一次函数f(x)=ax+b(a≠0)是否属于集合M?说明理由;
(2)设函数f(x)=logax(a>1)的图像与y=x的图像有公共点,试证明:f(x)=logax∈M.
查看答案和解析>>
科目:高中数学 来源:导练必修一数学苏教版 苏教版 题型:022
已学函数的定义域和值域
(1)一次函数f(x)=ax+b(a≠0):定义域为________,值域为________.
(2)反比例函数f(x)=![]() (k≠0):定义域为________,值域为________.
(k≠0):定义域为________,值域为________.
(3)二次函数f(x)=ax2+bx+c(a≠0):定义域为________,值域:当a>0时,为________;当a<0时,为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com