
【题目】已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1,![]() ).
).
(1)求椭圆C的方程;
(2)设与圆O:x2+y2=![]() 相切的直线l交椭圆C于A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
相切的直线l交椭圆C于A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
科目:高中数学 来源: 题型:
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象是由函数
的图象是由函数![]() 的图象经如下变换得到:先将
的图象经如下变换得到:先将![]() 图象上所有点的纵坐标伸长到原来的
图象上所有点的纵坐标伸长到原来的![]() 倍(横坐标不变),再将所得到的图象向右平移
倍(横坐标不变),再将所得到的图象向右平移![]() 个单位长度.
个单位长度.
(1)求函数![]() 的解析式,并求其图象的对称轴方程;
的解析式,并求其图象的对称轴方程;
(2)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() 、
、![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是空气质量的一个重要指标,我国
是空气质量的一个重要指标,我国![]() 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即![]() 日均值在
日均值在![]() 以下空气质量为一级,在
以下空气质量为一级,在![]() 之间空气质量为二级,在
之间空气质量为二级,在![]() 以上空气质量为超标.如图是某地
以上空气质量为超标.如图是某地![]() 月
月![]() 日到
日到![]() 日
日![]() 日均值(单位:
日均值(单位:![]() )的统计数据,则下列叙述不正确的是( )
)的统计数据,则下列叙述不正确的是( )
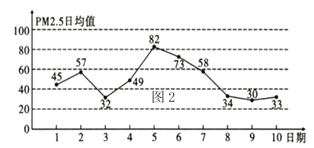
A.从![]() 日到
日到![]() 日,
日,![]() 日均值逐渐降低
日均值逐渐降低
B.这![]() 天的
天的![]() 日均值的中位数是
日均值的中位数是![]()
C.这![]() 天中
天中![]() 日均值的平均数是
日均值的平均数是![]()
D.从这![]() 天的日均
天的日均![]() 监测数据中随机抽出一天的数据,空气质量为一级的概率是
监测数据中随机抽出一天的数据,空气质量为一级的概率是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(示意),公路AM、AN围成的是一块顶角为钝角α的角形耕地,其中![]() .在该块土地中
.在该块土地中![]() 处有一小型建筑,经测量,它到公路
处有一小型建筑,经测量,它到公路![]() 、
、![]() 的距离
的距离![]() 、
、![]() 分别为
分别为![]() ,
,![]() .现要过点
.现要过点![]() 修建一条直线公路
修建一条直线公路![]() ,将三条公路围成的区域
,将三条公路围成的区域![]() 建成一个工业园.设
建成一个工业园.设![]() ,
,![]()
![]() ,其中
,其中![]() .
.

(1)试建立![]() 间的等量关系;
间的等量关系;
(2)为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年被称为“新高考元年”,随着上海、浙江两地顺利实施“语数外+3”新高考方案,新一轮的高考改革还将继续在全国推进.辽宁地区也将于2020年开启新高考模式,今年秋季入学的高一新生将面临从物理、化学、生物、政治、历史、地理等6科中任选三科(共20种选法)作为自己将来高考“语数外+3”新高考方案中的“3”.某地区为了顺利迎接新高考改革,在某学校理科班的200名学生中进行了“学生模拟选科数据”调查,每个学生只能从表格中的20种课程组合选择一种学习.模拟选课数据统计如下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 |
人数 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
组合学科 | 物政历 | 物政地 | 物历地 | 化生政 | 化生历 | 化生地 | 化政历 |
人数 | 5人 | 0人 | 5人 | …… | 40人 | …… | …… |
序号 | 15 | 16 | 17 | 18 | 19 | 20 | |
组合学科 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | 总计 |
人数 | …… | …… | …… | …… | …… | …… | 200人 |
为了解学生成绩与学生模拟选课之间的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析。
(1)样本中选择组合6号“物生历”的有多少人?样本中同时选择学习物理和历史的有多少人?
(2)从样本选择学习物理且学习历史的学生中随机抽取3人,求这3人中至少有2人还要学习生物的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将给定的一个数列![]() :
:![]() ,
,![]() ,
,![]() ,…按照一定的规则依顺序用括号将它分组,则可以得到以组为单位的序列.如在上述数列中,我们将
,…按照一定的规则依顺序用括号将它分组,则可以得到以组为单位的序列.如在上述数列中,我们将![]() 作为第一组,将
作为第一组,将![]() ,
,![]() 作为第二组,将
作为第二组,将![]() ,
,![]() ,
,![]() 作为第三组,…,依次类推,第
作为第三组,…,依次类推,第![]() 组有
组有![]() 个元素(
个元素(![]() ),即可得到以组为单位的序列:
),即可得到以组为单位的序列:![]() ,
,![]() ,
,![]() ,…,我们通常称此数列为分群数列.其中第1个括号称为第1群,第2个括号称为第2群,第3个数列称为第3群,…,第
,…,我们通常称此数列为分群数列.其中第1个括号称为第1群,第2个括号称为第2群,第3个数列称为第3群,…,第![]() 个括号称为第
个括号称为第![]() 群,从而数列
群,从而数列![]() 称为这个分群数列的原数列.如果某一个元素在分群数列的第
称为这个分群数列的原数列.如果某一个元素在分群数列的第![]() 个群众,且从第
个群众,且从第![]() 个括号的左端起是第
个括号的左端起是第![]() 个,则称这个元素为第
个,则称这个元素为第![]() 群众的第
群众的第![]() 个元素.已知数列1,1,3,1,3,9,1,3,9,27,…,将数列分群,其中,第1群为(1),第2群为(1,3),第3群为(1,3,
个元素.已知数列1,1,3,1,3,9,1,3,9,27,…,将数列分群,其中,第1群为(1),第2群为(1,3),第3群为(1,3,![]() ),…,以此类推.设该数列前
),…,以此类推.设该数列前![]() 项和
项和![]() ,若使得
,若使得![]() 成立的最小
成立的最小![]() 位于第
位于第![]() 个群,则
个群,则![]() ( )
( )
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com