
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为:
的方程为:![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(1)求证:直线![]() 恒过定点;
恒过定点;
(2)当直线![]() 被圆
被圆![]() 截得的弦长最短时,求直线
截得的弦长最短时,求直线![]() 的方程;
的方程;
(3)在(2)的前提下,若![]() 为直线
为直线![]() 上的动点,且圆
上的动点,且圆![]() 上存在两个不同的点到点
上存在两个不同的点到点![]() 的距离为
的距离为![]() ,求点
,求点![]() 的横坐标的取值范围.
的横坐标的取值范围.
【答案】(1)证明见解析.
(2)![]() .
.
(3)![]() .
.
【解析】分析:(1)直线l可理解为过定点的直线系,求出直线恒过的定点;
(2)说明直线l被圆C截得的弦长最短时,圆心与定点连线与直线l垂直,求出斜率即可得到直线![]() 的方程;.
的方程;.
(3)问题可转化为以![]() 为圆心,
为圆心, ![]() 为半径画圆
为半径画圆![]() ,当圆
,当圆![]() 与圆
与圆![]() 相交时满足题意.
相交时满足题意.
详解:(1)![]() ,
,
由![]() 得
得![]() ,
,
即直线![]() 过定点M
过定点M![]() .
.
(![]() )方法一:由题意可知:圆心C:
)方法一:由题意可知:圆心C:![]() ,
,
![]()
![]() ,
,
又![]() 当所截弦长最短时,
当所截弦长最短时,![]()
![]() ,
,
![]() .
.
方法二:∵圆心![]() 到直线
到直线![]() 的距离,
的距离,
![]() ,
,
设弦长为![]() ,则
,则![]() ,
,
当所截弦长最短时, ![]() 取最大值,
取最大值,
∴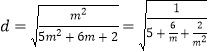 ,令
,令![]() ,
,
![]() .
.
令![]()
![]() ,
,
当![]() 时,
时, ![]() 取到最小值
取到最小值![]() .
.
此时![]() ,
, ![]() 取最大值,弦长取最小值,
取最大值,弦长取最小值,
直线上方程为![]() .
.
(![]() )设
)设![]() ,
,
当以![]() 为圆心,
为圆心, ![]() 为半径画圆
为半径画圆![]() ,当圆
,当圆![]() 与圆
与圆![]() 刚好相外切时,
刚好相外切时,
![]() ,
,
解得![]() 或
或![]() ,
,
由题意,圆![]() 与圆心有两个交点时符合题意,
与圆心有两个交点时符合题意,
∴点![]() 横坐标的取值范围为
横坐标的取值范围为![]() .
.


 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
【题目】2016年一交警统计了某段路过往车辆的车速大小与发生的交通事故次数,得到如下表所示的数据:
车速 |
|
|
|
|
|
事故次数 |
|
|
|
|
|
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测2017年该路段路况及相关安全设施等不变的情况下,车速达到![]() 时,可能发生的交通事故次数.
时,可能发生的交通事故次数.
(参考数据:![]() )
)
[参考公式: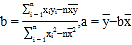 ]
]

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校高三毕业生报考体育专业学生的体重(单位:千克)情况,将他们的体重数据整理后得到如下频率分布直方图,已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
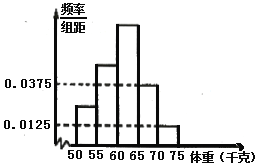
(Ⅰ)求该校报考体育专业学生的总人数![]() ;
;
(Ⅱ)已知A, ![]() 是该校报考体育专业的两名学生,A的体重小于55千克,
是该校报考体育专业的两名学生,A的体重小于55千克, ![]() 的体重不小于70千克,现从该校报考体育专业的学生中按分层抽样分别抽取体重小于55千克和不小于70千克的学生共6名,然后再从这6人中抽取体重小于55千克学生1人,体重不小于70千克的学生2人组成3人训练组,求A不在训练组且
的体重不小于70千克,现从该校报考体育专业的学生中按分层抽样分别抽取体重小于55千克和不小于70千克的学生共6名,然后再从这6人中抽取体重小于55千克学生1人,体重不小于70千克的学生2人组成3人训练组,求A不在训练组且![]() 在训练组的概率.
在训练组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)如图所示,已知以点![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切.过点
相切.过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 的中点,直线
的中点,直线![]() 与
与![]() 相交于点
相交于点![]() .
.
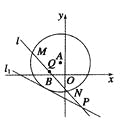
(1)求圆![]() 的方程;
的方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
(3)![]() 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
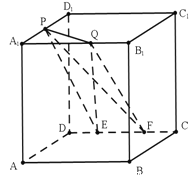
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上任意一点,
上任意一点,![]() ,
,![]() 为
为![]() 上任意两点,且
上任意两点,且![]() 的长为定值,则下面的四个值中不为定值的是( )
的长为定值,则下面的四个值中不为定值的是( )
A. 点![]() 到平面
到平面![]() 的距离B. 三棱锥
的距离B. 三棱锥![]() 的体积
的体积
C. 直线![]() 与平面
与平面![]() 所成的角D. 二面角
所成的角D. 二面角![]() 的大小
的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,且![]() =9,S6=60.
=9,S6=60.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn+1﹣bn=![]() (n∈N+)且b1=3,求数列
(n∈N+)且b1=3,求数列![]() 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三梭柱ABC﹣A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
(1)求证:E是AB中点;
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com