
【题目】现从某学校中选出![]() 名学生,统计了
名学生,统计了![]() 名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.
名学生一周的户外运动时间(分钟)总和,得到如图所示的频率分布直方图和统计表格.

(1)写出![]() 的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
的值,并估计该学校人均每周的户外运动时间(同一组数据用该组区间的中点值作代表);
(2)假设![]() ,则户外运动时长为
,则户外运动时长为![]() 的学生中,男生人数比女生人数多的概率.
的学生中,男生人数比女生人数多的概率.
(3)若![]() ,完成下列
,完成下列![]() 列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
列联表,并回答能否有90%的把握认为“每周至少运动130分钟与性别有关”?
每周户外运动时间不少于130分钟 | 每周户外运动时间少于130分钟 | 合计 | |
男 | |||
女 | |||
合计 |
附: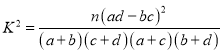 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)![]() ,
,![]() ,
,![]() ,112分钟;(2)
,112分钟;(2)![]() ;(3)列联表详见解析,没有90%的把握认为“每周至少运动130分钟与性别有关”.
;(3)列联表详见解析,没有90%的把握认为“每周至少运动130分钟与性别有关”.
【解析】
(1)根据频率分布直方图的面积和为1以及区间![]() 与
与![]() 间的比例关系列式求解即可.
间的比例关系列式求解即可.
(2)利用枚举法将所有可能的情况列举再求解即可.
(3)根据图表补全列联表,再求出![]() 分析即可.
分析即可.
(1)由人数比可得![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
该校人均户外运动时间为![]() 分钟.
分钟.
(2)设“户外运动时长为![]() 的男女人数分布”为总事件
的男女人数分布”为总事件![]() ,
,
![]()
![]() 共7种,
共7种,
“男生人数比女生人数多”为事件![]() ,包含
,包含![]() 共三个,
共三个,
则![]() .
.
(3)
每周户外运动时间不少于130分钟 | 每周户外运动时间少于130分钟 | 合计 | |
男 | 3 | 8 | 11 |
女 | 1 | 8 | 9 |
合计 | 4 | 16 | 20 |
![]() ,
,
所以没有90%的把握认为“每周至少运动130分钟与性别有关”.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得![]() 分).
分).
(1)设每轮游戏中出现“摸出两个都是红球”的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有关部门在某公交站点随机抽取了100名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟),将数据按![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 分组,绘制成如图所示的频率分布直方图.
分组,绘制成如图所示的频率分布直方图.
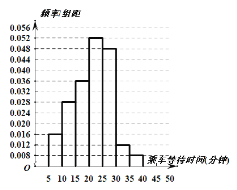
假设乘客乘车等待时间相互独立.
(1)求抽取的100名乘客乘车等待时间的中位数(保留一位小数);
(2)现从该车站等车的乘客中随机抽取4人,记等车时间在![]() 的人数为
的人数为![]() ,用频率估计概率,求随机变量
,用频率估计概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() ,若点
,若点![]() 为抛物线
为抛物线![]() 准线上的动点,给出以下命题:
准线上的动点,给出以下命题:
①当![]() 为正三角形时,
为正三角形时,![]() 的值为
的值为![]() ;
;
②存在![]() 点,使得
点,使得![]() ;
;
③若![]() ,则
,则![]() 等于
等于![]() ;
;
④![]() 的最小值为
的最小值为![]() ,则
,则![]() 等于
等于![]() 或
或![]() .
.
其中正确的是( )
A.①③④B.②③C.①③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前n项和为
的前n项和为![]() , ,且
, ,且![]() ,
,![]() ,.在①
,.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为F,P为其上一动点,设直线l与抛物线C相交于A,B两点,点
的焦点为F,P为其上一动点,设直线l与抛物线C相交于A,B两点,点![]() 下列结论正确的是( )
下列结论正确的是( )
A.|PM| +|PF|的最小值为3
B.抛物线C上的动点到点![]() 的距离最小值为3
的距离最小值为3
C.存在直线l,使得A,B两点关于![]() 对称
对称
D.若过A、B的抛物线的两条切线交准线于点T,则A、B两点的纵坐标之和最小值为2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,把
,把![]() 上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数
上各点横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图象,关于
的图象,关于![]() 有下述四个结论:
有下述四个结论:
(1)函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)当![]() ,且
,且![]() 时,
时,![]() ,则
,则![]() ;
;
(3)函数![]() (其中
(其中![]() )的最小值为
)的最小值为![]() .
.
其中正确结论的个数为( ).
A.1B.2C.3D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非典和新冠肺炎两场疫情告诉我们:应坚决杜绝食用野生动物,提倡文明健康,绿色环保的生活方式.在我国抗击新冠肺炎期间,某校开展一次有关病毒的网络科普讲座.高三年级男生60人,女生40人参加.按分层抽样的方法,在100名同学中选出5人,则男生中选出________人.再从此5人中选出两名同学作为联络人,则这两名联络人中男女都有的概率是________.(第1空2分,第2空3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com