
【题目】设事件A表示“关于x的一元二次方程x2+ax+b2=0有实根”,其中a,b为实常数. (Ⅰ)若a为区间[0,5]上的整数值随机数,b为区间[0,2]上的整数值随机数,求事件A发生的概率;
(Ⅱ)若a为区间[0,5]上的均匀随机数,b为区间[0,2]上的均匀随机数,求事件A发生的概率.
【答案】解:(Ⅰ)当a∈{0,1,2,3,4,5},b∈{0,1,2}时,共可以产生6×3=18个一元二次方程. 若事件A发生,则a 2﹣4b2≥0,即|a|≥2|b|.又a≥0,b≥0,所以a≥2b.
从而数对(a,b)的取值为(0,0),(1,0),(2,0),(2,1),(3,0),(3,1),(4,0),(4,1),(4,2),(5,0),(5,1),(5,2),共12组值.
所以P(A)= ![]() .
.
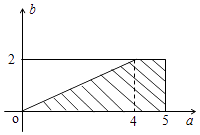
(Ⅱ)据题意,试验的全部结果所构成的区域为D={(a,b)|0≤a≤5,0≤b≤2},构成事件A的区域为A={(a,b)|0≤a≤5,0≤b≤2,a≥2b}.
在平面直角坐标系中画出区域A、D,如图,
其中区域D为矩形,其面积S(D)=5×2=10,
区域A为直角梯形,其面积S(A)= ![]() .
.
所以P(A)= ![]() .
.
【解析】(Ⅰ)本题是古典概型,首先明确事件的个数,利用公式解答;Ⅱ)本问是几何概型的求法,明确事件对应的区域面积,利用面积比求概率.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)对任意的x∈(﹣ ![]() ,
, ![]() )满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
A.![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() )
)
B.![]() f(
f( ![]() )<f(
)<f( ![]() )??
)??
C.f(0)>2f( ![]() )
)
D.f(0)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的左、右焦点为F1、F2 , 离心率为e.直线l:y=ex+a与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左、右焦点为F1、F2 , 离心率为e.直线l:y=ex+a与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设 ![]() =λ
=λ ![]() .
.
(1)证明:λ=1﹣e2;
(2)若λ= ![]() ,△MF1F2的周长为6;写出椭圆C的方程;
,△MF1F2的周长为6;写出椭圆C的方程;
(3)确定λ的值,使得△PF1F2是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在平面内![]() 是
是![]() 且
且![]() 的菱形
的菱形![]() 和
和![]() 都是正方形.将两个正方形分别沿
都是正方形.将两个正方形分别沿![]() 折起,使
折起,使![]() 与
与![]() 重合于点
重合于点![]() .设直线
.设直线![]() 过点
过点![]() 且垂直于菱形ABCD所在的平面,点
且垂直于菱形ABCD所在的平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 同侧(图②).
同侧(图②).
(1)求证:不管点![]() 如何运动都有
如何运动都有![]() 平面
平面![]() ;
;
(2)当线段![]() 时,求二面角
时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程是 ![]() =1,F1 , F2是它的左、右焦点,A,B为它的左、右顶点,l是椭圆的右准线,P是椭圆上一点,PA、PB分别交准线l于M,N两点.
=1,F1 , F2是它的左、右焦点,A,B为它的左、右顶点,l是椭圆的右准线,P是椭圆上一点,PA、PB分别交准线l于M,N两点.
(1)若P(0, ![]() ),求
),求 ![]() 的值;
的值;
(2)若P(x0 , y0)是椭圆上任意一点,求 ![]() 的值;
的值;
(3)能否将问题推广到一般情况,即给定椭圆方程是 ![]() =1(a>b>0),P(x0 , y0)是椭圆上任意一点,问
=1(a>b>0),P(x0 , y0)是椭圆上任意一点,问 ![]() 是否为定值?证明你的结论.
是否为定值?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)现有5名男生和3名女生.若从中选5人,且要求女生只有2名,站成一排,共有多少种不同的排法?
(2)从{﹣3,﹣2,﹣1,0,1,2,3,4}中任选三个不同元素作为二次函数y=ax2+bx+c的系数,问能组成多少条经过原点且顶点在第一象限或第三象限的抛物线?
(3)已知( ![]() +2x)n , 若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大项的系数.
+2x)n , 若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大项的系数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com