
【题目】对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() ,其中
,其中![]() 为自然对数的底数,则实数
为自然对数的底数,则实数![]() 的取值范围是______
的取值范围是______
【答案】![]()
【解析】
令![]() ,根据函数单调性可得f(x)∈[﹣1,e2],然后令g(x)=ax﹣ex,由x1≠x2,g(x1)=g(x2),可知y=mlnm﹣m与y=g(x)的图象有2个交点,结合函数单调性即可求解.
,根据函数单调性可得f(x)∈[﹣1,e2],然后令g(x)=ax﹣ex,由x1≠x2,g(x1)=g(x2),可知y=mlnm﹣m与y=g(x)的图象有2个交点,结合函数单调性即可求解.
令![]() ,则
,则![]() ,
,
当![]() 时,f′(x)=lnx<0,∴f(x)单调递减,
时,f′(x)=lnx<0,∴f(x)单调递减,
当1<x<e2,f′(x)=lnx>0,∴f(x)单调递增,
∵![]() ,故函数f(x)的值域为
,故函数f(x)的值域为![]() .
.
令g(x)=ax﹣ex,则g′(x)=a﹣ex,且x1≠x2,g(x1)=g(x2),
①当a≤0时,g′(x)=a﹣ex<0恒成立,∴g(x)在R上单调递减,
与x1≠x2,g(x1)=g(x2),矛盾
②当a>0时,当x>lna时,g′(x)=a﹣ex<0,∴函数g(x)单调递减,
当x<lna时,g′(x)=a﹣ex>0,∴函数g(x)单调递增,
∵当x→﹣∞时,g(x)→﹣∞,当x→+∞时,g(x)→﹣∞且
g(x)max=g(lna)=alna﹣a,
∴当x1≠x2时,若g(x1)=g(x2)=mlnm﹣m,
则y=mlnm与y=g(x)有2个不同的交点,
∴alna﹣a>e2=e2lne2﹣e2,又a>0
由f(x)的单调性可得a>e2,
∴实数a的取值范围为:(e2,+∞).
故答案为:(e2,+∞)


科目:高中数学 来源: 题型:
【题目】空中有一气球,在它的正西方A点测得它的仰角为45°,同时在它南偏东60°的B点,测得它的仰角为30°,已知A、B两点间的距离为107米,这两个观测点均离地1米,则测量时气球离地的距离是_____米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行一次“环保知识竞赛”,全校学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为![]() 分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
(Ⅰ)写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(Ⅱ)在选取的样本中,从竞赛成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到广场参加环保知识的志愿宣传活动,求所抽取的
名同学到广场参加环保知识的志愿宣传活动,求所抽取的![]() 名同学来自同一组的概率.
名同学来自同一组的概率.
(Ⅲ)在(Ⅱ)的条件下,设![]() 表示所抽取的
表示所抽取的![]() 名同学中来自第
名同学中来自第![]() 组的人数,求
组的人数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
组别 | 分组 | 频数 | 频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
合计 |
|
|

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ( x R ,且 e 为自然对数的底数).
( x R ,且 e 为自然对数的底数).
⑴ 判断函数 f x 的单调性与奇偶性;
⑵是否存在实数 t ,使不等式![]() 对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大豆是我国主要的农作物之一,因此,大豆在农业发展中占有重要的地位,随着农业技术的不断发展,为了使大豆得到更好的种植,就要进行超级种培育研究.某种植基地培育的“超级豆”种子进行种植测试:选择一块营养均衡的可种植![]() 株的实验田地,每株放入三粒“超级豆”种子,且至少要有一粒种子发芽这株豆苗就能有效成活,每株豆成活苗可以收成大豆
株的实验田地,每株放入三粒“超级豆”种子,且至少要有一粒种子发芽这株豆苗就能有效成活,每株豆成活苗可以收成大豆![]() .已知每粒豆苗种子成活的概率为
.已知每粒豆苗种子成活的概率为![]() (假设种子之间及外部条件一致,发芽相互没有影响).
(假设种子之间及外部条件一致,发芽相互没有影响).
(Ⅰ)求恰好有3株成活的概率;
(Ⅱ)记成活的豆苗株数为![]() ,收成为
,收成为![]() ,求随机变量
,求随机变量![]() 分布列及
分布列及![]() 数学期望
数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
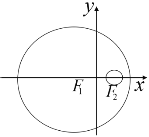
【题目】如图,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若动圆
,若动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过直线![]() 上的点
上的点![]() 作圆
作圆![]() 的两条切线,设切点分别是
的两条切线,设切点分别是![]() ,
,![]() ,若直线
,若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com