已知

(其中
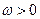
)的最小正周期为
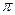
。
小题1:求
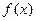
的单调递增区间;
小题2:在
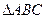
中,
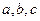
分别是角A,B,C的对边,已知
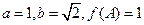
,求角C。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
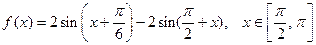
.
(1)若
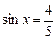
,求函数
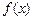
的值;(2)求函数
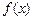
的值域;
(3)求满足
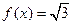
的自变量
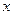
的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)已知函数
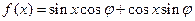
(其中
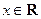
,
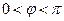
).
(1)求函数
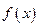
的最小正周期;(2)若函数
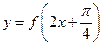
的图像关于直线
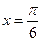
对称,求
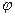
的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
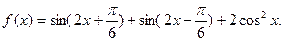
.
(I)求
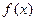
的最小正周期及最大值;
(II)求使
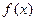
≥2的
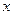
的取值范围
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
若
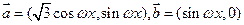
,其中
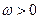
,记函数
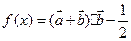
(1)若
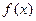
的图像中两条相邻对称轴间的距离
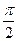
,求
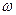
及
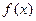
的单调减区间。
(2)在(1)的条件下,且
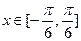
,求最大值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
求下列函数的定义域:
(1)y=lgsin(cosx);(2)y=
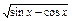
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
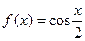
,下面四个等式
①
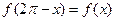
②
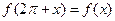
③
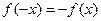
④
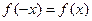
成立的个数是___________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分)已知向量
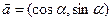
,
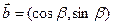
,
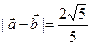
.
(Ⅰ)求
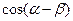
的值;
(Ⅱ)若
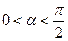
,
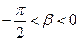
, 且
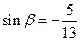
, 求
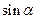
的值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数y=sinxcosx+
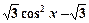
的图象的一个对称中心是 ( )
查看答案和解析>>

 (其中
(其中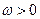 )的最小正周期为
)的最小正周期为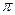 。
。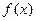 的单调递增区间;
的单调递增区间;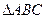 中,
中,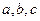 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知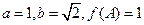 ,求角C。
,求角C。 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案