练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知等差数列{an}的前3项和为6，前8项和为－4.

    (1)求数列{an}的通项公式；

    (2)设bn＝(4－an)qn－1 (q≠0，n∈N*)，求数列{bn}的前n项和Sn.

    【答案】见解析

    【解析】解 (1)设数列{an}的公差为d，

    由已知，得解得

    故an＝3－(n－1)＝4－n.

    (2)由(1)可得bn＝n·qn－1，

    于是Sn＝1·q0＋2·q1＋3·q2＋…＋n·qn－1.

    若q≠1，将上式两边同时乘以q，得

    qSn＝1·q1＋2·q2＋…＋(n－1)·qn－1＋n·qn.

    两式相减，得(q－1)Sn＝nqn－1－q1－q2－…－qn－1

    ＝nqn－＝.

    于是，Sn＝.

    若q＝1，则Sn＝1＋2＋3＋…＋n＝.

    综上，Sn＝

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数在时取得极小值．

    （1）求实数的值；

    （2）是否存在区间，使得在该区间上的值域为？若存在，求出的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图．

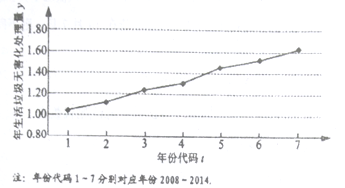
    （1）由折线图看出，可用线性回归模型拟合与的关系，请用相关系数加以说明；

    （2）建立关于的回归方程（系数精确到0．01），预测2016年我国生活垃圾无害化处理量．

    参考数据： ， ， ， ．

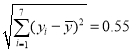    参考公式：相关系数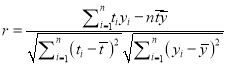

    回归方程中， ， ．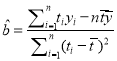

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=，其中a∈R.

    （I）当a=1时，求曲线y=f（x）在原点处的切线方程；

    （II）求f（x）的极值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（， ）为奇函数，且相邻两对称轴间的距离为.

    （1）当时，求的单调递减区间；

    （2）将函数的图象沿轴方向向右平移个单位长度，再把横坐标缩短到原来的（纵坐标不变），得到函数的图象.当时，求函数的值域.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设关于θ的方程cosθ＋sinθ＋a＝0在区间(0,2π)内有相异的两个实根α、β.

    (1)求实数a的取值范围；

    (2)求α＋β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】比较下列各组中两个值的大小 ：

    (1)ln0.3，ln2； (2)loga3.1，loga5.2(a>0，且a≠1)；

    (3)log30.2，log40.2； (4)log3π，logπ3.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f(x)的最小值为1，且f(0)＝f(2)＝3.

    (1)求f(x)的解析式；

    (2)若f(x)在区间[2a，a＋1]上不单调，求实数a的取值范围；

    (3)在区间[－1,1]上，y＝f(x)的图象恒在y＝2x＋2m＋1的图象上方，试确定实数m的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有3名男生，4名女生，在下列不同要求下，求不同的排列方法种数：

    （1）选其中5人排成一排

    （2）全体排成一排，甲不站在排头也不站在排尾

    （3）全体排成一排，男生互不相邻

    （4）全体排成一排，甲、乙两人中间恰好有3人

    查看答案和解析>>

    同步练习册答案