
【题目】已知函数![]() (
(![]() 为实数,
为实数,![]() ,
,![]() ).
).
(1)当函数![]() 的图象过点
的图象过点![]() ,且方程
,且方程![]() 有且只有一个根,求
有且只有一个根,求![]() 的表达式;
的表达式;
(2)在(1)的条件下,当![]() 时,
时,![]() 是单调函数,求实数
是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若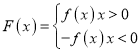 ,当
,当![]() ,
,![]() ,
,![]() ,且函数
,且函数![]() 为偶函数时,试判断
为偶函数时,试判断![]() 能否大于
能否大于![]() ?
?
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】若数列![]() 对任意
对任意![]() 满足
满足![]() ,下面给出关于数列
,下面给出关于数列![]() 的四个命题:①
的四个命题:①![]() 可以是等差数列,②
可以是等差数列,②![]() 可以是等比数列;③
可以是等比数列;③![]() 可以既是等差又是等比数列;④
可以既是等差又是等比数列;④![]() 可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点.
的中点.
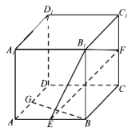
(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ∥平面
∥平面![]() ?请证明你的结论;
?请证明你的结论;
(3)求直线![]() 与平面
与平面![]() 所成角的余弦值;
所成角的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口的水深![]() (米)是时间
(米)是时间![]() (
(![]() ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过长期观测,![]() 可近似的看成是函数
可近似的看成是函数![]()
(1)根据以上数据,求出![]() 的解析式;
的解析式;
(2)若船舶航行时,水深至少要![]() 米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区为了了解本年度数学竞赛成绩情况,从中随机抽取了![]() 个学生的分数作为样本进行统计,按照
个学生的分数作为样本进行统计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图所示,已知得分在
的分组作出频率分布直方图如图所示,已知得分在![]() 的频数为20,且分数在70分及以上的频数为27.
的频数为20,且分数在70分及以上的频数为27.
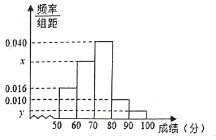
(1)求样本容量![]() 以及
以及![]() ,
,![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数的解析式为f(x)=![]() (a∈R).
(a∈R).
(1)试求a的值;
(2)写出f(x)在[0,1]上的解析式;
(3)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(1)求![]() 及
及![]() 的解析式及定义域;
的解析式及定义域;
(2)如函数![]() 在区间
在区间![]() 上为单调函数,求实数
上为单调函数,求实数![]() 的范围.
的范围.
(3)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=![]() .
.
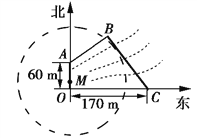
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com