
分析 (1)先分别求出A点、B点的直角坐标,由此能求出|AB|的长.
(2)设C的直角坐标为C(a,b),由直线垂直的性质和两点点距离公式列出方程组求出B点直角坐标,由此能求出C点的极坐标.
解答 解:(1)∵在极坐标系内,A(2,$\frac{π}{4}$),
∴x=2cos$\frac{π}{4}$=$\sqrt{2}$,y=2sin$\frac{π}{4}$=$\sqrt{2}$,
∴A点直角坐标为A($\sqrt{2},\sqrt{2}$),
∵在极坐标系内,B(2,$\frac{5π}{4}$),
∴$x=2cos\frac{5π}{4}$=-$\sqrt{2}$,y=2sin$\frac{5π}{4}$=-$\sqrt{2}$,
∴B点直角坐标B(-$\sqrt{2}$,-$\sqrt{2}$),
∴|AB|=$\sqrt{(\sqrt{2}+\sqrt{2})^{2}+(\sqrt{2}+\sqrt{2})^{2}}$=4.
(2)∵A($\sqrt{2},\sqrt{2}$),B(-$\sqrt{2}$,-$\sqrt{2}$),
∴kAB=1,∵A,B是等边三角形的两个顶点,
∴kOC=-1,
设C的直角坐标为C(a,b),
则$\left\{\begin{array}{l}{\frac{b}{a}=-1}\\{(a-\sqrt{2})^{2}+(b-\sqrt{2})^{2}=(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\sqrt{6}}\\{b=-\sqrt{6}}\end{array}\right.$或$\left\{\begin{array}{l}{a=-\sqrt{6}}\\{b=\sqrt{6}}\end{array}\right.$,
当$\left\{\begin{array}{l}{a=\sqrt{6}}\\{b=-\sqrt{6}}\end{array}\right.$时,$ρ=\sqrt{6+6}=2\sqrt{3}$,θ=$\frac{7π}{4}$,C点极坐标为:(2$\sqrt{3}$,$\frac{7π}{4}$)
当$\left\{\begin{array}{l}{a=-\sqrt{6}}\\{b=\sqrt{6}}\end{array}\right.$时,$ρ=\sqrt{6+6}=2\sqrt{3}$,$θ=\frac{3π}{4}$,C点的极坐标为:(2$\sqrt{3}$,$\frac{3π}{4}$).
∴C点的极坐标为:(2$\sqrt{3}$,$\frac{3π}{4}$),(2$\sqrt{3}$,$\frac{7π}{4}$).
点评 本题考查线段长的求法,考查点的极坐标的求法,是基础题,解题时要认真审题,注意极坐标和直角坐标的互化及直线垂直的性质和两点点距离公式的合理运用.


科目:高中数学 来源: 题型:解答题
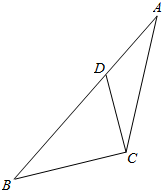 如图,在△ABC中,已知点D在AB边上,且$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,sin∠ACB=$\frac{5\sqrt{7}}{14}$,AC=$\sqrt{7}$,AD=1.
如图,在△ABC中,已知点D在AB边上,且$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,sin∠ACB=$\frac{5\sqrt{7}}{14}$,AC=$\sqrt{7}$,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4,∠PAB=60°
在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4,∠PAB=60° 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,$AB=\sqrt{2}a$.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点,若AD=PA=a,$AB=\sqrt{2}a$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com