
【题目】已知命题a2x2+ax﹣2=0在[﹣1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p”或“q”是假命题,求a的取值范围.
【答案】解:由题意a≠0.
若p正确,a2x2+ax﹣2=(ax+2)(ax﹣1)=0的解为 ![]() 或-
或- ![]()
若方程在[﹣1,1]上有解,只需满足| ![]() |≤1或|﹣
|≤1或|﹣ ![]() |≤1
|≤1
∴a≥1或a≤﹣1
即a∈(﹣∞,﹣1]∪[1,+∞)
若q正确,即只有一个实数x满足x2+2ax+2a≤0,
则有△=4a2﹣8a=0,即a=0或2
若p或q是假命题,则p和q都是假命题,
有 ![]()
所以a的取值范围是(﹣1,0)∪(0,1)
【解析】对方程a2x2+ax﹣2=0进行因式分解是解决该题的关键,得出方程的根(用a表示出).利用根在[﹣1,1]上,得出关于a的不等式,求出命题p为真的a的范围,利用x2+2ax+2a≤0相应的二次方程的判别式等于0得出关于a的方程,求出a,再根据“p或q”是假命题得出a的范围.
【考点精析】关于本题考查的复合命题的真假,需要了解“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真才能得出正确答案.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】已知命题:①函数![]() 的值域是
的值域是![]() ;
;
②为了得到函数![]() 的图象,只需把函数
的图象,只需把函数![]() 图象上的所有点向右平移
图象上的所有点向右平移![]() 个单位长度;
个单位长度;
③当![]() 或
或![]() 时,幂函数
时,幂函数![]() 的图象都是一条直线;
的图象都是一条直线;
④已知函数 ,若
,若![]() 互不相等,且
互不相等,且![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .
.
其中正确的命题个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
①从1,2,3,4,5中任取2个不同的数,事件![]() “取到的2个数之和为偶数”,事件
“取到的2个数之和为偶数”,事件![]() “取到的
“取到的
2个数均为偶数”,则![]() ;
;
②某班共有45名学生,其中30名男同学,15名女同学,老师随机抽查了5名同学的作业,用![]() 表示抽查到的女生的人数,则
表示抽查到的女生的人数,则![]() ;
;
③设随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
④由直线![]() ,
,![]() ,曲线
,曲线![]() 及
及![]() 轴所围成的图形的面积是
轴所围成的图形的面积是![]() .
.
其中所有正确结论的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地合作农场的果园进入盛果期,果农利用互联网电商渠道销售苹果,苹果单果直径不同则单价不同,为了更好的销售,现从该合作农场果园的苹果树上随机摘下了50个苹果测量其直径,经统计,其单果直径分布在区间![]() 内(单位:
内(单位:![]() ),统计的茎叶图如图所示:
),统计的茎叶图如图所示:

(Ⅰ)按分层抽样的方法从单果直径落在![]() ,
,![]() 的苹果中随机抽取6个,则从
的苹果中随机抽取6个,则从![]() ,
,![]() 的苹果中各抽取几个?
的苹果中各抽取几个?
(Ⅱ)从(Ⅰ)中选出的6个苹果中随机抽取2个,求这两个苹果单果直径均在![]() 内的概率;
内的概率;
(Ⅲ)以此茎叶图中单果直径出现的频率代表概率,若该合作农场的果园有20万个苹果约5万千克待出售,某电商提出两种收购方案:方案![]() :所有苹果均以5.5元/千克收购;方案
:所有苹果均以5.5元/千克收购;方案![]() :按苹果单果直径大小分3类装箱收购,每箱装25个苹果,定价收购方式为:单果直径在
:按苹果单果直径大小分3类装箱收购,每箱装25个苹果,定价收购方式为:单果直径在![]() 内按35元/箱收购,在
内按35元/箱收购,在![]() 内按45元/箱收购,在
内按45元/箱收购,在![]() 内按55元/箱收购.包装箱与分拣装箱费用为5元/箱(该费用由合作农场承担).请你通过计算为该合作农场推荐收益最好的方案.
内按55元/箱收购.包装箱与分拣装箱费用为5元/箱(该费用由合作农场承担).请你通过计算为该合作农场推荐收益最好的方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,点![]() 实施变换
实施变换![]() 后,对应点为
后,对应点为![]() ,给出以下命题:
,给出以下命题:
①圆![]() 上任意一点实施变换
上任意一点实施变换![]() 后,对应点的轨迹仍是圆
后,对应点的轨迹仍是圆![]() ;
;
②若直线![]() 上每一点实施变换
上每一点实施变换![]() 后,对应点的轨迹方程仍是
后,对应点的轨迹方程仍是![]() 则
则![]() ;
;
③椭圆![]() 上每一点实施变换
上每一点实施变换![]() 后,对应点的轨迹仍是离心率不变的椭圆;
后,对应点的轨迹仍是离心率不变的椭圆;
④曲线![]() 上每一点实施变换
上每一点实施变换![]() 后,对应点的轨迹是曲线
后,对应点的轨迹是曲线![]() ,
,![]() 是曲线
是曲线![]() 上的任意一点,
上的任意一点,![]() 是曲线
是曲线![]() 上的任意一点,则
上的任意一点,则![]() 的最小值为
的最小值为![]() .
.
以上正确命题的序号是___________________(写出全部正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若在区间[0,1]上有最大值1和最小值-2.求a,b的值;
(2)在(1)条件下,若在区间![]() 上,不等式f(x)
上,不等式f(x)![]()
![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是椭圆上一点.
是椭圆上一点.
(1)求椭圆的标准方程;
(2)过椭圆右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,
两点,![]() 是直线
是直线![]() 上任意一点.
上任意一点.
证明:直线![]() 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. 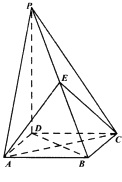
(1)求证:平面AEC⊥平面PDB;
(2)当PD=2AB,且E为PB的中点,求二面角B﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,将
,将![]() 的图象向右平移两个单位长度,得到函数
的图象向右平移两个单位长度,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且仅有一个实根,求
上有且仅有一个实根,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,设
对称,设![]() ,已知
,已知![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com