
【题目】某奶茶店对某时间段的奶茶销售量及其价格进行调查,统计出售价![]() 元和销售量
元和销售量![]() 杯之间的一组数据如下表所示:
杯之间的一组数据如下表所示:
价格 | 5 | 5.5 | 6.5 | 7 |
销售量 | 12 | 10 | 6 | 4 |
通过分析,发现销售量![]() 对奶茶的价格
对奶茶的价格![]() 具有线性相关关系.
具有线性相关关系.
(1)求销售量![]() 对奶茶的价格
对奶茶的价格![]() 的回归直线方程;
的回归直线方程;
(2)欲使销售量为13杯,则价格应定为多少?
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点. 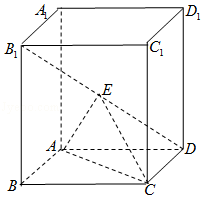
(Ⅰ)证明:平面ACE⊥平面ABCD;
(Ⅱ)若二面角D﹣AE﹣C为60°,AA1=AB=1,求三棱锥C﹣AED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的圆心为
的圆心为 ![]() 的圆心为N,一动圆与圆M内切,与圆N外切.
的圆心为N,一动圆与圆M内切,与圆N外切.
(1)求动圆圆心P的轨方迹方程;
(2)设A,B分别为曲线P与x轴的左右两个交点,过点 ![]() 的直线
的直线 ![]() 与曲线P交于C,D两点,若
与曲线P交于C,D两点,若 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①若![]() ,则
,则![]() ;
;
②已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是
的取值范围是![]() ;
;
③已知![]() 是平面上一定点,
是平面上一定点,![]() 是平面上不共线的三个点,动点
是平面上不共线的三个点,动点![]() 满足
满足![]() ,
,![]() ,则
,则![]() 的轨迹一定通过
的轨迹一定通过![]() 的重心;
的重心;
④在![]() 中,
中,![]() ,边长
,边长![]() 分别为
分别为![]() ,则
,则![]() 只有一解;
只有一解;
⑤如果△ABC内接于半径为![]() 的圆,且
的圆,且![]()
则△ABC的面积的最大值![]() ;
;
其中正确的序号为_______________________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 ![]() 以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A,B两点.
以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A,B两点.
(1)写出直线l的极坐标方程与曲线C的普通方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在著名的汉诺塔问题中有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上:①每次只能移动一个金属片;②在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n个金属片从1号针移到3号针最少需要移动的次数记为f(n),则f(6)=( ) 
A.31
B.33
C.63
D.65
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=x﹣ln x﹣2.
(Ⅰ)求函数 f ( x) 的最小值;
(Ⅱ)如果不等式 x ln x+(1﹣k)x+k>0(k∈Z)在区间(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各两张,让孩子从盒子里任取3张卡片,按卡片上的最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量X的分布列及数学期望;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com