
分析 先求出0≤m≤$\frac{3}{10}$,$\frac{2}{5}≤n≤1$,再由$\left\{\begin{array}{l}{m≥n-\frac{2}{5}}\\{n≥m}\\{m+\frac{7}{10}≥n}\end{array}\right.$,$\left\{\begin{array}{l}{n-\frac{2}{5}≥m}\\{n≤m+\frac{7}{10}}\\{\;}\end{array}\right.$,$\left\{\begin{array}{l}{n-\frac{2}{5}≥m}\\{m+\frac{7}{10}≥n-\frac{2}{5}}\\{m+\frac{7}{10}≤n}\end{array}\right.$三种情况进行发类讨论经,能求出M∩N的“长度”的最小值.
解答 解:∵数集M=$\{x\left|{m≤x≤m+\frac{7}{10}}\right.\}$,N=$\{x\left|{n-\frac{2}{5}≤x≤n}\right.\}$且集合M,N都是集合{x|0≤x≤1}的子集,
∴$\left\{\begin{array}{l}{m≥0}\\{m+\frac{7}{10}≤1}\end{array}\right.$,∴0≤m≤$\frac{3}{10}$,
$\left\{\begin{array}{l}{n-\frac{2}{5}≥0}\\{n≤1}\end{array}\right.$,∴$\frac{2}{5}≤n≤1$,
①若$\left\{\begin{array}{l}{m≥n-\frac{2}{5}}\\{n≥m}\\{m+\frac{7}{10}≥n}\end{array}\right.$,则M∩N={x|m≤x≤n},
此时集合M∩N的“长度”为:n-m∈[$\frac{1}{10}$,$\frac{2}{5}$]
此时合M∩N的“长度”的最小值是$\frac{1}{10}$;
②若$\left\{\begin{array}{l}{n-\frac{2}{5}≥m}\\{n≤m+\frac{7}{10}}\\{\;}\end{array}\right.$,则M∩N={x|n-$\frac{2}{5}<x<n$},
此时集合M∩N的“长度”为:n-m=$\frac{2}{5}$,
此时M∩N的“长度”的最小值是$\frac{2}{5}$;
③若$\left\{\begin{array}{l}{n-\frac{2}{5}≥m}\\{m+\frac{7}{10}≥n-\frac{2}{5}}\\{m+\frac{7}{10}≤n}\end{array}\right.$,则M∩N={x|$n-\frac{2}{5}$$≤x≤m+\frac{7}{10}$},
此时集合M∩N的“长度”为:m-n+$\frac{11}{10}$∈[$\frac{1}{10}$,$\frac{2}{5}$]
此时M∩N的“长度”的最小值是$\frac{1}{10}$.
综上,M∩N的“长度”的最小值是$\frac{1}{10}$.
故答案为:$\frac{1}{10}$.
点评 本题考查交集的长度的最小值的求法,是中档题,解题时要认真审题,注意交集性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (3)(4) | C. | (2)(3) | D. | (1)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈A,2x∈B | B. | ?x∉A,2x∉B | C. | ?x∈A,2x∉B | D. | ?x∉A,2x∉B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
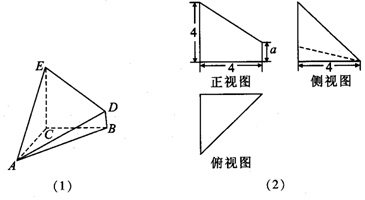
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com