
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集非空,求
的解集非空,求![]() 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线.当t∈(0,14]时,曲线是二次函数图象的一部分,当t∈[14,40]时,曲线是函数![]() (
(![]() 且
且![]() )图象的一部分.根据专家研究,当注意力指数p大于等于80时听课效果最佳.
)图象的一部分.根据专家研究,当注意力指数p大于等于80时听课效果最佳.

(1)试求![]() 的函数关系式;
的函数关系式;
(2)一道数学难题,讲解需要22分钟,问老师能否经过合理安排在学生听课效果最佳时讲完?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.
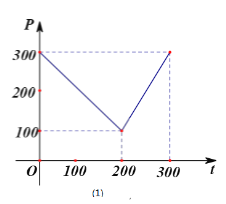
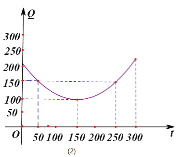
(1)写出图(1)表示的市场售价与时间的函数关系式![]() ;写出图(2)表示的种植成本与时间的函数关系式
;写出图(2)表示的种植成本与时间的函数关系式![]() ;
;
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上函数![]() 的图象关于图象上点(1,0)对称,f(x)对任意的实数x都有
的图象关于图象上点(1,0)对称,f(x)对任意的实数x都有![]() 且f(3)=0,则函数y=f(x)在区间
且f(3)=0,则函数y=f(x)在区间![]() 上的零点个数最少有( )
上的零点个数最少有( )
A.2020个B.1768个C.1515个D.1514个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com