
【题目】已知椭圆C: ![]() =1(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
=1(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(Ⅰ)求椭圆C的标准方程和长轴长;
(Ⅱ)设F为椭圆C的左焦点,P为直线x=﹣3上任意一点,过点F作直线PF的垂线交椭圆C于M,N,记d1 , d2分别为点M和N到直线OP的距离,证明:d1=d2 .
【答案】解:(Ⅰ)由题意可知椭圆的焦点在x轴上,2c=4,c=2, ![]() =2b,
=2b,
由a2=b2+c2 , 解得a2=6,b2=2,
∴椭圆C的标准方程为 ![]() ,椭圆C的长轴长为
,椭圆C的长轴长为 ![]() .
.
(Ⅱ)由(Ⅰ)可知点F的坐标为(﹣2,0),设点P的坐标为(﹣3,m),
则直线PF的斜率 ![]() ,
,
当m≠0时,直线MN的斜率 ![]() ,直线MN的方程是x=my﹣2,
,直线MN的方程是x=my﹣2,
当m=0时,直线MN的方程是x=﹣2,也符合x=my﹣2的形式,
设M(x1 , y1),N(x2 , y2),将直线MN的方程与椭圆C的方程联立,
得 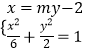 ,消去x,得(m2+3)y2﹣4my﹣2=0,
,消去x,得(m2+3)y2﹣4my﹣2=0,
其判别式△=16m2+8(m2+3)>0,
所以 ![]() ,
, ![]() ,
, ![]() ,
,
设T为线段MN的中点,则点T的坐标为 ![]() ,
,
所以直线OT的斜率 ![]() ,
,
又直线OP的斜率 ![]() ,
,
所以点T在直线OP上,
由三角形全等的判定和性质可知:d1=d2
【解析】(Ⅰ)由椭圆的性质可知:c=2, ![]() =2b,即可求得a和b的值,求得椭圆方程;(Ⅱ)由(Ⅰ)求得直线MN的方程,代入椭圆方程,由韦达定理及中点坐标公式可知求得MN的中点T,由kOT=kOP , 由三角形全等的判定和性质可知:d1=d2 .
=2b,即可求得a和b的值,求得椭圆方程;(Ⅱ)由(Ⅰ)求得直线MN的方程,代入椭圆方程,由韦达定理及中点坐标公式可知求得MN的中点T,由kOT=kOP , 由三角形全等的判定和性质可知:d1=d2 .
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣axlnx(a∈R)在x=1处的切线方程为y=bx+1+
﹣axlnx(a∈R)在x=1处的切线方程为y=bx+1+ ![]() (b∈R).
(b∈R).
(1)求a,b的值;
(2)证明:f(x)< ![]() .
.
(3)若正实数m,n满足mn=1,证明: ![]() +
+ ![]() <2(m+n).
<2(m+n).
查看答案和解析>>
科目:高中数学 来源: 题型:
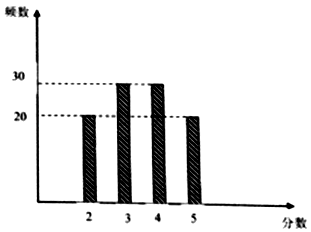
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.
(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;
(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).
(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).
服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
等级 | 不好 | 较好 | 优良 |
奖惩标准(元) | ﹣1000 | 2000 | 3000 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣ ![]() )+2cos2x,将函数y=f(x)的图象向右平移
)+2cos2x,将函数y=f(x)的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
A.(﹣ ![]() ,1)
,1)
B.(﹣ ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数,﹣π<α<0),曲线C2的参数方程为
(α为参数,﹣π<α<0),曲线C2的参数方程为  (t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1的极坐标方程和曲线C2的普通方程;
(2)射线θ=﹣ ![]() 与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1 , 则双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)短轴的端点P(0,b)、Q(0,﹣b),长轴的一个端点为M,AB为经过椭圆中心且不在坐标轴上的一条弦,若PA、PB的斜率之积等于﹣
(a>b>0)短轴的端点P(0,b)、Q(0,﹣b),长轴的一个端点为M,AB为经过椭圆中心且不在坐标轴上的一条弦,若PA、PB的斜率之积等于﹣ ![]() ,则P到直线QM的距离为
,则P到直线QM的距离为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品计划提价,现有四种方案,方案(Ⅰ)先提价m%,再提价n%;方案(Ⅱ)先提价n%,再提价m%;方案(Ⅲ)分两次提价,每次提价( ![]() )%;方案(Ⅳ)一次性提价(m+n)%,已知m>n>0,那么四种提价方案中,提价最多的是( )
)%;方案(Ⅳ)一次性提价(m+n)%,已知m>n>0,那么四种提价方案中,提价最多的是( )
A.Ⅰ
B.Ⅱ
C.Ⅲ
D.Ⅳ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D,E分别在边AB,BC上,且AB=3AD,BC=2BE.
(Ⅰ)用向量 ![]() ,
, ![]() 表示
表示 ![]() .
.
(Ⅱ)设AB=6,AC=4,A=60°,求线段DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com