
 ,若f(x1)+f(2x2)=1(其中x1,x2均大于2),则f(x1x2)的最小值为 .
,若f(x1)+f(2x2)=1(其中x1,x2均大于2),则f(x1x2)的最小值为 . 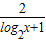 ,f(a)+f(2b)=2-2(
,f(a)+f(2b)=2-2(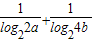 )=1,所以能够推导出log22a+log24b≥8,所以log2ab≥5,由此知f(ab)=1-
)=1,所以能够推导出log22a+log24b≥8,所以log2ab≥5,由此知f(ab)=1- ≥
≥ .故f(x1x2)的最小值为
.故f(x1x2)的最小值为 .
. ,若f(a)+f(2b)=1,其中a>2,b>2.
,若f(a)+f(2b)=1,其中a>2,b>2. ,
, )=1.
)=1. =
= .
.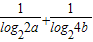 )≥4得
)≥4得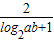 ≥
≥ .(等号当且仅当a=2b时成立).
.(等号当且仅当a=2b时成立). .
. .
.

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2011-2012学年江西省南昌十六中高一(上)12月月考数学试卷(解析版) 题型:选择题
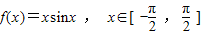 ,若f(x1)>f(x2),则下列不等式必定成立的是( )
,若f(x1)>f(x2),则下列不等式必定成立的是( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省衢州市常山一中高三(上)第三次月考数学试卷(文科)(解析版) 题型:选择题
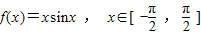 ,若f(x1)>f(x2),则下列不等式必定成立的是( )
,若f(x1)>f(x2),则下列不等式必定成立的是( )查看答案和解析>>
科目:高中数学 来源:2007-2008学年广东省广州市高三调研数学试卷(理科)(解析版) 题型:选择题
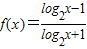 ,若f(x1)+f(2x2)=1,(其中x1,x2均大于2),则f(x1x2)的最小值为( )
,若f(x1)+f(2x2)=1,(其中x1,x2均大于2),则f(x1x2)的最小值为( )



查看答案和解析>>
科目:高中数学 来源:2011年江苏省苏北四市高三第二次联考数学模拟试卷(一)(解析版) 题型:填空题
 ,若f(x1)+f(2x2)=1(其中x1,x2均大于2),则f(x1x2)的最小值为 .
,若f(x1)+f(2x2)=1(其中x1,x2均大于2),则f(x1x2)的最小值为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com