
【题目】设![]() 为正项数列
为正项数列![]() 的前
的前![]() 项和,且
项和,且![]() .数列
.数列![]() 满足:
满足:![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,问是否存在整数
,问是否存在整数![]() ,使数列
,使数列![]() 为递增数列?若存在求
为递增数列?若存在求![]() 的值,若不存在说明理由.
的值,若不存在说明理由.
【答案】(1) ![]() ;
;![]() . (2)
. (2) ![]() (3)存在,
(3)存在,![]()
【解析】
(1)先由题意求出![]() ,再由
,再由![]() 时,
时,![]() ,推出数列
,推出数列![]() 是以
是以![]() 为公差的等差数列,求出
为公差的等差数列,求出![]() 的通项;根据
的通项;根据![]() ,得到
,得到![]() ,推出数列
,推出数列![]() 是以
是以![]() 为公比的等比数列,进而可求出数列
为公比的等比数列,进而可求出数列![]() 的通项公式;
的通项公式;
(2)先由(1)得到![]() ,根据错位相减法,即可求出结果;
,根据错位相减法,即可求出结果;
(3)先由(1)得![]() ,假设存在
,假设存在![]() ,满足
,满足![]() 为递增数列,得到
为递增数列,得到![]() 对任意
对任意![]() 恒成立,列出不等式
恒成立,列出不等式![]() ,分别讨论
,分别讨论![]() 为奇数,
为奇数,![]() 为偶数两种情况,即可求出结果.
为偶数两种情况,即可求出结果.
(1)当![]() 时,解得
时,解得![]() ,
,
当![]() 时,由
时,由![]() ,及
,及![]() ,
,
相减得![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍);即数列
(舍);即数列![]() 是以
是以![]() 为公差的等差数列,
为公差的等差数列,
故![]() ;
;
由![]() 得
得![]() ,所以数列
,所以数列![]() 是以
是以![]() 为公比的等比数列,
为公比的等比数列,
又![]() ,故
,故![]() ,所以
,所以![]() .
.
(2)由(1)得![]() .
.
所以![]() ,
,
![]() ,
,
相减得![]()
从而![]() ;
;
(3)由(1)得![]() ,若存在
,若存在![]() ,满足
,满足![]() 为递增数列,
为递增数列,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
由![]()
得![]()
当![]() 为奇数时,由
为奇数时,由![]() 得
得![]() ,
,
当![]() 为偶数时,由
为偶数时,由![]() 得
得![]() ,
,
![]() ,故
,故![]() .
.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】如图,某小区准备将闲置的一直角三角形地块开发成公共绿地,图中![]() .设计时要求绿地部分(如图中阴影部分所示)有公共绿地走道
.设计时要求绿地部分(如图中阴影部分所示)有公共绿地走道![]() ,且两边是两个关于走道
,且两边是两个关于走道![]() 对称的三角形(
对称的三角形(![]() 和
和![]() ).现考虑方便和绿地最大化原则,要求点
).现考虑方便和绿地最大化原则,要求点![]() 与点
与点![]() 均不重合,
均不重合,![]() 落在边
落在边![]() 上且不与端点
上且不与端点![]() 重合,设
重合,设![]() .
.
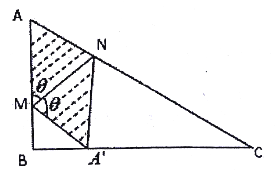
(1)若![]() ,求此时公共绿地的面积;
,求此时公共绿地的面积;
(2)为方便小区居民的行走,设计时要求![]() 的长度最短,求此时绿地公共走道
的长度最短,求此时绿地公共走道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过点
,过点![]() 的直线与抛物线
的直线与抛物线![]() 相切,设第一象限的切点为
相切,设第一象限的切点为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于两点
相交于两点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆过点
为直径的圆过点![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震释放出的能量![]() (单位:焦耳)与地震里氏震级
(单位:焦耳)与地震里氏震级![]() 之间的关系为
之间的关系为![]() .
.
(1)已知地震等级划分为里氏![]() 级,根据等级范围又分为三种类型,其中小于
级,根据等级范围又分为三种类型,其中小于![]() 级的为“小地震”,介于
级的为“小地震”,介于![]() 级到
级到![]() 级之间的为“有感地震”,大于
级之间的为“有感地震”,大于![]() 级的为“破坏性地震”若某次地震释放能量约
级的为“破坏性地震”若某次地震释放能量约![]() 焦耳,试确定该次地震的类型;
焦耳,试确定该次地震的类型;
(2)2008年汶川地震为里氏![]() 级,2011年日本地震为里氏
级,2011年日本地震为里氏![]() 级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取
级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小电子产品2018年的价格为9元/件,年销量为![]() 件,经销商计划在2019年将该电子产品的价格降为
件,经销商计划在2019年将该电子产品的价格降为![]() 元/件(其中
元/件(其中![]() ),经调查,顾客的期望价格为5元/件,经测算,该电子产品的价格下降后年销量新增加了
),经调查,顾客的期望价格为5元/件,经测算,该电子产品的价格下降后年销量新增加了![]() 件(其中常数
件(其中常数![]() ).已知该电子产品的成本价格为4元/件.
).已知该电子产品的成本价格为4元/件.
(1)写出该电子产品价格下降后,经销商的年收益![]() 与实际价格
与实际价格![]() 的函数关系式:(年收益=年销售收入-成本)
的函数关系式:(年收益=年销售收入-成本)
(2)设![]() ,当实际价格最低定为多少时,仍然可以保证经销商2019年的收益比2018年至少增长20%?
,当实际价格最低定为多少时,仍然可以保证经销商2019年的收益比2018年至少增长20%?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(
,(![]() ,
,![]() ,
,![]() )的部分图像如图所示.
)的部分图像如图所示.
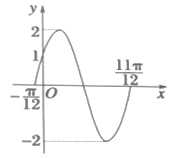
(1)求函数![]() 的解析式及
的解析式及![]() 图像的对称轴方程;
图像的对称轴方程;
(2)把函数![]() 图像上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移
图像上点的横坐标扩大到原来的2倍(纵坐标不变),再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于x的方程
的图象,求关于x的方程![]() 在
在![]() 时所有的实数根之和.
时所有的实数根之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com